题目内容

14．已知函数f（x）=x2-6x-9，则函数f（x）在x∈（1，4）的值域是[-18，-14）．

分析 利用二次函数在x∈（1，4）的单调性的性质即可求得答案．

解答 解：∵f（x）=x2-6x-9=（x-3）2-18，
∴其对称轴x=3穿过区间（1，4）
∴函数在x∈（1，4）时，f（x）min=f（3）=-18，
又f（x）在（1，3]上递减，在[3，4）递增，
f（1）=-14，f（4）=-17，f（4）＜f（1），
∴该函数的值域为[-18，-14），
故答案为[-18，-14）．

点评 本题考查二次函数的性质，着重考查二次函数的单调性与最值，考查分析解决问题的能力，属于基础题．

练习册系列答案
相关题目
4．曲线y=ex在点A（0，1）处的切线斜率为1．
5．如果关于x的不等式2kx2+kx-$\frac{3}{8}$＜0对一切实数x都成立，那么k的取值范围是（-3，0]．
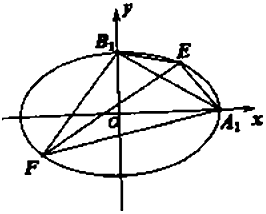2．如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率是$\frac{\sqrt{3}}{2}$，且过点（$\sqrt{3}$，$\frac{1}{2}$）．设点A1，B1分别是椭圆的右顶点和上顶点，如图所示过 点A1，B1引椭圆C的两条弦A1E、B1F．
（1）求椭圆C的方程；
（2）若直线A1E与B1F的斜率是互为相反数．
①求直线EF的斜率k0 ②设直线EF的方程为y=k0x+b（-1≤b≤1）设△A1EF、△B1EF的面积分别为S1和S2，求S1+S2的取值范围．
9．已知函数f（x）是定义在R上的增函数，若f（a2-a）＞f（2a2-4a），则实数a的取值范围是（　　）
A．（-∞，0）B．（0，3）C．（3，+∞）D．（-∞，0）∪（3，+∞）
19．求函数f（x）=log${\;}_{\frac{1}{3}}$（x2-5x+4）的定义域和单调区间．
6．下列命题中真命题的序号为（1）．
（1）命题“?x＞0，x2-x≤0”的否定是“?x＞0，x2-x＞0．”
（2）若A＞B，则sinA＞sinB．
（3）已知数列{an}，则“an，an+1，an+2成等比数列”是“$a_{n+1}^2={a_n}{a_{n+2}}$”的充要条件
（4）已知函数$f（x）=lgx+\frac{1}{lgx}$，则函数f（x）的最小值为2．
3．数轴上点A，B分别对应-1、2，则向量$\overrightarrow{AB}$的长度是（　　）
A．-1B．2C．1D．3
4．过抛物线C：y2=4x的焦点F的直线l交C于A，B两点，点M（-1，2），若$\overrightarrow{MA}•\overrightarrow{MB}=0$，则直线l的斜率k=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网