题目内容
16.(1)已知复数z=3+ai(a∈R)且|z|<4,求实数a的取值范围.(2)记复数z的共轭复数记作$\overline z$,已知$({1+2i})\overline z=4+3i$,求z.
分析 (1)利用复数模的计算公式即可得出.
(2)利用复数的运算法则、共轭复数的定义即可得出.
解答 解:(1)复数z=3+ai(a∈R)且|z|<4,∴$\sqrt{{3}^{2}+{a}^{2}}$<4,解得$-\sqrt{7}<a<\sqrt{7}$.
∴实数a的取值范围$(-\sqrt{7},\sqrt{7})$.
(2)∵$({1+2i})\overline z=4+3i$,∴(1-2i)(1+2i)$\overline{z}$=(4+3i)(1-2i),∴5$\overline{z}$=10-5i,$\overline{z}$=2-i.
∴z=2+i.
点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
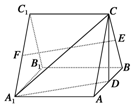 如图,直三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明:
如图,直三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明: