题目内容
3.下列四个命题中,真命题的是( )| A. | 空间中两组对边分别相等的四边形为平行四边形 | |
| B. | 所有梯形都有外接圆 | |
| C. | 所有的质数的平方都不是偶数 | |
| D. | 不存在一个奇数,它的立方是偶数 |
分析 由平行四边形的定义判断A;根据只有等腰梯形有外接圆判断B;举例说明C错误;由命题的等价命题判断D.
解答 解:由平行四边形的定义可知A错误;
只有等腰梯形有外接圆,可知B错误;
2为质数,2的平方为偶数,C错误;
命题“不存在一个奇数,它的立方是偶数”?“所有奇数的立方是奇数”为真命题.
故选:D.
点评 本题考查命题的真假判断与应用,考查学生对基础知识与基础概念的理解与掌握,是基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
11.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=-4x+3sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
8.与x轴相切且和半圆x2+y2=4(0≤y≤2)内切的动圆圆心的轨迹方程是( )
| A. | x2=-4(y-1)(0<y≤1) | B. | x2=4(y-1)(0<y≤1) | C. | x2=4(y+1)(0<y≤1) | D. | x2=-2(y-1)(0<y≤1) |
12.已知直线l:$\sqrt{3}x-y+4=0$与圆x2+y2=16交于A,B两点,则$\overrightarrow{AB}$在x轴正方向上投影的绝对值为( )
| A. | $4\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
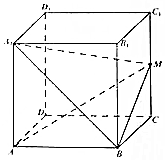 已知棱长为1的正方体ABCD-A1B1C1D1中,M是棱CC1的中点,则三棱锥A1-ABM的体积为$\frac{1}{6}$.
已知棱长为1的正方体ABCD-A1B1C1D1中,M是棱CC1的中点,则三棱锥A1-ABM的体积为$\frac{1}{6}$.