题目内容
13.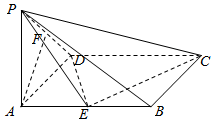 已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.(1)求证:AF∥平面PEC;
(2)求证:平面PEC⊥平面PDC.
分析 (1)取PC中点G,连接FG、EG,可证四边形AEGF为平行四边形,可得AF∥EG,由线面平行的判定定理可得;
(2)由线面垂直的判定定理可证AF⊥平面PCD,进而可得EG⊥平面PCD,由面面垂直的判定定理可得.
解答 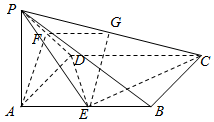 证明:(1)取PC中点G,连接FG、EG,
证明:(1)取PC中点G,连接FG、EG,
在△PCD中由中位线可得FG∥CD且FG=$\frac{1}{2}$CD,
又AE∥CD且AE=$\frac{1}{2}$CD,∴FG∥AE且FG=AE,
∴四边形AEGF为平行四边形,∴AF∥EG,
又AF?平面PEC,EG?平面PEC,
∴AF∥平面PEC;
(2)由PA⊥平面ABCD,PA=AD=1,可得△PAD为等腰直角三角形,
再由F分别是PD的中点可得AF⊥PD,再由PA⊥平面ABCD可得PA⊥CD,
由底面ABCD是矩形可得CD⊥AB,∴CD⊥平面PAD,∴CD⊥AF,
∴AF⊥平面PCD,∴EG⊥平面PCD,由EG?平面PEC,
∴平面PEC⊥平面PDC.
点评 本题考查直线和平面平行和垂直的判定,作出辅助线并逐步寻找满足判定定理的条件是解决问题的关键,属中档题.

练习册系列答案
相关题目
3.设数列{an}中,已知a1=1,an=1+$\frac{1}{{a}_{n-1}}$(n>1),则a4=( )
| A. | $\frac{8}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
4.若△ABC中,a=4,A=45°,B=60°,则边b的值为( )
| A. | $\sqrt{3}$+1 | B. | 2$\sqrt{3}$+1 | C. | 2$\sqrt{6}$ | D. | 2+2$\sqrt{3}$ |
8.已知△ABC是锐角三角形,则点P(cosC-sinA,sinA-cosB)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知向量$\overrightarrow{a}$=(1,-1),$\overrightarrow{b}$=(-1,2),若($\overrightarrow{a}$-λ$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则实数λ的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
2.执行如图所示的程序框图,若输入的x=0,则输出的S的值为( )


| A. | 22 | B. | 37 | C. | 38 | D. | 63 |