题目内容
1.若以数列{an}中相邻的三项ak,ak+1,ak+2(k∈N*)为三边长能构成三角形,则称这个三角形为ak的“伴生三角形”.(Ⅰ)若公差为2的等差数列{an}的每一项an都有“伴生三角形”,求首项a1的取值范围;
(Ⅱ)若(Ⅰ)中的数列{an}的“伴生三角形”中存在直角三角形,求首项a1的所有可能取值.
分析 (I).由已知可得:an=2n+a1-2⇒an<an+1<an+2,…,依此类推即可得出;
(II).由(I)可知a1>2,an=2n+a1-2,利用{an}的“伴生三角形”中存在直角三角形及其勾股定理、数列通项公式即可得出.
解答 解:(I).由已知,an=2n+a1-2⇒an<an+1<an+2,
故有an+an+1>an+2⇒an>an+2-an+1=2⇒a1>4-2n(恒成立).
∴a1>2.
(II).由(I)可知a1>2,an=2n+a1-2,
∵{an}的“伴生三角形”中存在直角三角形,∴$a_n^2+a_{n+1}^2=a_{n+2}^2⇒a_n^2=({{a_{n+2}}-{a_{n+1}}})({{a_{n+2}}+{a_{n+1}}})$,
故${(2n+{a_1}-2)^2}=2(4n+2{a_1}+2)$$4{n^2}+(4{a_1}-16)n+{a_1}^2-8{a_1}=0$,化为(2n+a1)(2n+a1-8)=0,
∵a1>2,∴a1=8-2n,∴n=1,2a1=6或a1=4.
∴首项a1的所有可能取值是6或4.
点评 本题考查了新定义“伴生三角形”、勾股定理、数列通项公式、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知|$\overrightarrow{a}$|=6$\sqrt{3}$,|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=-9,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
16.请阅读问题1的解答过程,然后借鉴问题1的解题思路完成问题2的解答:
问题1:已知数集A={a1,a2,…an}(1≤a1<a2<…<an,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A.若数集{a1,2,3,a4}具有性质P,求a1,a4的值.
问题2:已知数集A={a1,a2,…an}(0≤a1<a2<…<an,n≥2)具有性质P:
对任意的i,j(1≤i≤j≤n),ai+aj与aj-ai两数中至少有一个属于A.若数集{a1,1,3,a4}具有性质P,求a1,a4的值.
问题1:已知数集A={a1,a2,…an}(1≤a1<a2<…<an,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A.若数集{a1,2,3,a4}具有性质P,求a1,a4的值.
| 解:对于集合中最大的数a4,因为a4×a4>a4,3×a4>a4,2×a4>a4. 所以$\frac{a_4}{a_4}$,$\frac{a_4}{3}$,$\frac{a_4}{2}$都属于该集合. 又因为1≤a1<2<3<a4,所以$\frac{a_4}{a_4}<\frac{a_4}{3}<\frac{a_4}{2}<{a_4}$. 所以${a_1}=\frac{a_4}{a_4}=1$,$\frac{a_4}{3}=2,\frac{a_4}{2}=3$,故a1=1,a4=6. |
对任意的i,j(1≤i≤j≤n),ai+aj与aj-ai两数中至少有一个属于A.若数集{a1,1,3,a4}具有性质P,求a1,a4的值.
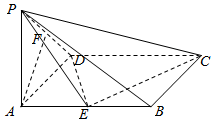 已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.