题目内容
5.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(-2,4),那么$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是$\sqrt{5}$.分析 计算$\overrightarrow{a}•\overrightarrow{b}$,|$\overrightarrow{b}$|,代入数量级的投影公式计算.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=3×(-2)+4×4=10.
|$\overrightarrow{b}$|=$\sqrt{4+16}$=2$\sqrt{5}$.
∴$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为|$\overrightarrow{a}$|•cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\sqrt{5}$.
故答案为$\sqrt{5}$.
点评 本题考查了平面向量的数量级运算,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
16.请阅读问题1的解答过程,然后借鉴问题1的解题思路完成问题2的解答:
问题1:已知数集A={a1,a2,…an}(1≤a1<a2<…<an,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A.若数集{a1,2,3,a4}具有性质P,求a1,a4的值.
问题2:已知数集A={a1,a2,…an}(0≤a1<a2<…<an,n≥2)具有性质P:
对任意的i,j(1≤i≤j≤n),ai+aj与aj-ai两数中至少有一个属于A.若数集{a1,1,3,a4}具有性质P,求a1,a4的值.
问题1:已知数集A={a1,a2,…an}(1≤a1<a2<…<an,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),aiaj与$\frac{a_j}{a_i}$两数中至少有一个属于A.若数集{a1,2,3,a4}具有性质P,求a1,a4的值.
| 解:对于集合中最大的数a4,因为a4×a4>a4,3×a4>a4,2×a4>a4. 所以$\frac{a_4}{a_4}$,$\frac{a_4}{3}$,$\frac{a_4}{2}$都属于该集合. 又因为1≤a1<2<3<a4,所以$\frac{a_4}{a_4}<\frac{a_4}{3}<\frac{a_4}{2}<{a_4}$. 所以${a_1}=\frac{a_4}{a_4}=1$,$\frac{a_4}{3}=2,\frac{a_4}{2}=3$,故a1=1,a4=6. |
对任意的i,j(1≤i≤j≤n),ai+aj与aj-ai两数中至少有一个属于A.若数集{a1,1,3,a4}具有性质P,求a1,a4的值.
20.设D是△ABC所在平面内一点,$\overrightarrow{AB}$=-2$\overrightarrow{DC}$,则( )
| A. | $\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | B. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{3}{2}$$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AB}$ | D. | $\overrightarrow{BD}$=$\frac{3}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ |
14.执行如图程序框图,如果输入的N的值是6,那么输出的p的值是( )


| A. | 105 | B. | 115 | C. | 120 | D. | 720 |
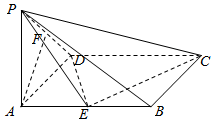 已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.