题目内容
已知两点A（-3，4），B（3，2），过点P（2，-1）的直线l与线段AB有公共点，求直线l的斜率的取值范围．
考点：直线的斜率
专题：直线与圆
分析：如图，由于直线l与线段AB有公共点且过点P（2，-1），可知直线l的倾斜角介于直线PB与直线PA的倾斜角之间
当直线l的倾斜角小于90°时，有k≥kPB，当直线l的倾斜角大于90°时，有k≤kPA，利用斜率计算公式即可得出．
当直线l的倾斜角小于90°时，有k≥kPB，当直线l的倾斜角大于90°时，有k≤kPA，利用斜率计算公式即可得出．
解答：
解：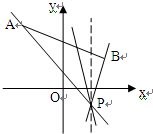
如图，
∵直线l与线段AB有公共点且过点P（2，-1）
∴直线l的倾斜角介于直线PB与直线PA的倾斜角之间
当直线l的倾斜角小于90°时，有k≥kPB，
当直线l的倾斜角大于90°时，有k≤kPA，
而kPA=
=-1，kPB=
=3．
∴直线l的斜率k的取值范围是（-∞，-1]∪[3，+∞）．
如图，∵直线l与线段AB有公共点且过点P（2，-1）
∴直线l的倾斜角介于直线PB与直线PA的倾斜角之间
当直线l的倾斜角小于90°时，有k≥kPB，
当直线l的倾斜角大于90°时，有k≤kPA，
而kPA=
| 4-(-1) |
| -3-2 |
| 2-(-1) |
| 3-2 |
∴直线l的斜率k的取值范围是（-∞，-1]∪[3，+∞）．
点评：本题考查了斜率计算公式、斜率与倾斜角的关系，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
设集合M={x|x=k•90°，k∈Z}，N={x|x=k•45°+90°，k∈Z}，则必有（ ）
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
