题目内容
求圆心在直线2x-y-3=0上，且过点A（5，2）和点B（3，-2）的圆的方程．
考点：圆的一般方程
专题：直线与圆
分析：根据条件可设圆心C（a，2a-3），半径为r，则圆的方程为 （x-a）2+（y-2a+3）2=r2，把点A（5，2）和点B（3，-2）的坐标代入方程，求出a及r的值，即得所求的圆的方程．
解答：
解：∵圆心在直线2x-y-3=0上，
∴可设圆心C（a，2a-3），半径为r，
则圆的方程为
（x-a）2+（y-2a+3）2=r2，
把点A（5，2）和点B（3，-2）的坐标代入方程，得
（5-a）2+（2-2a+3）2=r2 ①，
（3-a）2+（-2-2a+3）2=r2 ②，
由①②可得
a=2，r2=10
故所求的圆的方程为
（x-2）2+（y-1）2=10．
∴可设圆心C（a，2a-3），半径为r，
则圆的方程为
（x-a）2+（y-2a+3）2=r2，
把点A（5，2）和点B（3，-2）的坐标代入方程，得
（5-a）2+（2-2a+3）2=r2 ①，
（3-a）2+（-2-2a+3）2=r2 ②，
由①②可得
a=2，r2=10
故所求的圆的方程为
（x-2）2+（y-1）2=10．
点评：本题考查圆的标准方程的形式，直线和圆的位置关系，直线和圆相交的性质．
练习册系列答案
相关题目
若命题“?x0∈R，x02-3mx0+9＜0”为真命题，则实数m的取值范围是（ ）
| A、[-2，2] |
| B、（-2，2） |
| C、（-∞，-2]∪[2，+∞） |
| D、（-∞，-2）∪（2，+∞） |
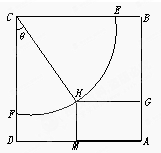某体育馆拟用运动场的边角地建一个矩形的健身室（如图所示），ABCD是一块边长为50m的正方形地皮，扇形CEF是运动场的一部分，其半径为40m，矩形AGHM就是拟建的健身室，其中G、M分别在AB和AD上，设矩形AGHM的面积为S，∠HCF=θ，请将S表示为θ的函数，并指出当点H在何处时，该健身室的面积最大，最大面积是多少？