题目内容
已知sinα+cosα=
，求sinαcosα及sin4α+cos4α
| 2 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：将已知等式两边平方，利用完全平方公式及同角三角函数间的基本关系化简，求出sinαcosα的值，sin4α+cos4α利用完全平方公式变形，将各自的值代入计算即可求出值．
解答：
解：∵sinα+cosα=
，
∴（sinα+cosα）2=2，即sin2α+cos2α+2sinαcosα=2，
整理得：1+2sinαcosα=2，即sinαcosα=
，
则sin4α+cos4α=（sin2α+cos2α）2-2sin2αcos2α=1-2（sinαcosα）2=1-
=
．
| 2 |
∴（sinα+cosα）2=2，即sin2α+cos2α+2sinαcosα=2，
整理得：1+2sinαcosα=2，即sinαcosα=
| 1 |
| 2 |
则sin4α+cos4α=（sin2α+cos2α）2-2sin2αcos2α=1-2（sinαcosα）2=1-
| 1 |
| 2 |
| 1 |
| 2 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
停车场一排12个车位，停8辆车，空位连在一起的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
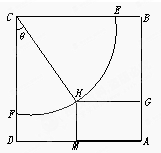某体育馆拟用运动场的边角地建一个矩形的健身室（如图所示），ABCD是一块边长为50m的正方形地皮，扇形CEF是运动场的一部分，其半径为40m，矩形AGHM就是拟建的健身室，其中G、M分别在AB和AD上，设矩形AGHM的面积为S，∠HCF=θ，请将S表示为θ的函数，并指出当点H在何处时，该健身室的面积最大，最大面积是多少？