题目内容
13．已知角α的终边上一点P（1，-2），则$\frac{sinα+2cosα}{sinα-cosα}$=0．分析 由条件利用任意角的三角函数的定义，求得所给式子的值．
解答 解：∵角α的终边上一点P（1，-2），∴sinα=$\frac{-2}{\sqrt{5}}$，cosα=$\frac{1}{\sqrt{5}}$，
∴$\frac{sinα+2cosα}{sinα-cosα}$=$\frac{\frac{-2}{\sqrt{5}}+2•\frac{1}{\sqrt{5}}}{\frac{-2}{\sqrt{5}}-\frac{1}{\sqrt{5}}}$=0，
故答案为：0．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
3．已知不等式组$\left\{\begin{array}{l}{x+y-2\sqrt{2}≥0}\\{x≤2\sqrt{2}}\\{y≤2\sqrt{2}}\end{array}\right.$表示平面区域Ω，过区域Ω中的任意一个点P，作圆x2+y2=1的两条切线且切点分别为A，B，当△PAB的面积最小时，cos∠APB的值为（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
4．函数y=$\frac{1}{\sqrt{{a}^{2}-{x}^{2}}}$，那么y′等于（ ）
| A． | -$\frac{\sqrt{{a}^{2}-{x}^{2}}}{a}$ | B． | $\frac{1}{2}$（a2-x2）${\;}^{\frac{3}{2}}$ | C． | x（a2-x2）${\;}^{-\frac{3}{2}}$ | D． | -$\frac{1}{2}$（a2-x2）${\;}^{\frac{3}{2}}$ |
1．复数z=（-2+i）i，则复数z的共轭复数是（ ）
| A． | -2+i | B． | -2-i | C． | -1+2i | D． | -1-2i |
18．在区间（0，1）内任取两个数x，y，则满足y≥2x概率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
2．
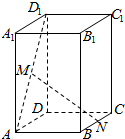如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，AA1=2，AB=1，M为AD1的中点，N在BC上，且MN∥平面DCC1D1，则BN的长为（ ）
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，AA1=2，AB=1，M为AD1的中点，N在BC上，且MN∥平面DCC1D1，则BN的长为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
3．已知复数z的共轭复数为$\overline z$，且$\overline z=\frac{2}{1+i}$，则|z|等于（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 2 $\sqrt{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |