题目内容
函数y=
的单调减区间和图象的对称中心分别为( )
| x+2 |
| x-1 |
| A、(-∞,0),(0,+∞),(1,1) |
| B、(-∞,-1),(-1,+∞),(1,0) |
| C、(-∞,1),(1,+∞),(1,0) |
| D、(-∞,1),(1,+∞),(1,1) |
考点:函数的单调性及单调区间
专题:函数的性质及应用
分析:由图象直接写出函数的单调区间;写出函数y=
的对称中心然后根据平移得到函数y=
的对称中心,
| 1 |
| x |
| x+2 |
| x-1 |
解答:
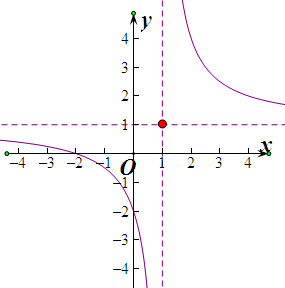 解:∵y=
解:∵y=
=1+
,x≠1
画出函数的图象如图所示,
由图象可知函数的单调减区间是(-∞,1),(1,+∞),
∵y=
的对称中心为(0,0)
∴.y=
=1+
的图象时由y=
的图象先向右平移一个单位,再向上平移1个单位得到的,
故对称中心为(1,1)
故选:D
 解:∵y=
解:∵y=| x+2 |
| x-1 |
| 3 |
| x-1 |
画出函数的图象如图所示,
由图象可知函数的单调减区间是(-∞,1),(1,+∞),
∵y=
| 1 |
| x |
∴.y=
| x+2 |
| x-1 |
| 3 |
| x-1 |
| 1 |
| x |
故对称中心为(1,1)
故选:D
点评:本题考查了函数的图象的变化问题,根据函数图象的变化,由熟悉的反比例函数图象得到题中分式函数的图象,从而得到函数的值域、单调区间和对称性,解答此题的关键是对函数解析式的变形,书写单调区间时学生容易取并集而出错,此题是基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
若函数f(x)=x+
(x>3),则f(x)的最小值为( )
| 1 |
| x-3 |
| A、3 | B、4 | C、5 | D、6 |
已知平面上两点M(-5,0)和N(5,0),若直线上存在点P使|PM|-|PN|=6,则称该直线为“单曲型直线”,下列直线中是“单曲型直线”的是( )
①y=x+1; ②y=2; ③y=
x; ④y=2x+1.
①y=x+1; ②y=2; ③y=
| 4 |
| 3 |
| A、①③ | B、①② | C、②③ | D、③④ |
定义在R上的奇函数f(x)满足f(x+3)=f(x),当0<x≤1时,f(x)=2x,则f (2015)=( )
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|