题目内容
14.cos(-375°)的值为( )| A. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $-\frac{{\sqrt{6}-\sqrt{2}}}{4}$ |
分析 利用诱导公式化为cos15°,进一步化为cos(45°-30°),展开两角差的余弦得答案.
解答 解:cos(-375°)=cos375°=cos15°=cos(45°-30°)
=cos45°cos30°+sin45°sin30°-$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$.
故选:C.
点评 本题考查利用诱导公式化简求值,考查了两角差余弦的应用,是基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
12.某高校大一新生的五名同学打算参加学校组织的“小草文学社”、“街舞俱乐部”、“足球之家”、“骑行者”四个社团.若毎个社团至少一名同学参加,每名同学至少参加一个社团且只能参加一个社团,其中同学甲不参加“街舞俱乐部”,则这五名同学不同的参加方法的种数为( )
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
2.已知函数f(x)的图象关于(1,1)对称,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,f(x)+2=$\frac{2}{f(\sqrt{x+1})}$,若g(x)=f(x)-t(x+1)为定义在(-1,3)上的函数,则关于g(x)的零点个数的叙述中错误的是( )
| A. | g(x)可能没有零点 | B. | g(x)可能有1个零点 | C. | g(x)可能有2个零点 | D. | g(x)可能有3个零点 |
6.有4个不同的球,四个不同的盒子,把球全部放入盒内,恰有两个盒不放球,共有( )种放法.
| A. | 114 | B. | 96 | C. | 84 | D. | 48 |
3.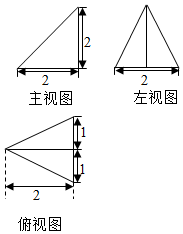 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
4.已知$α∈(0,\frac{π}{2})$,且$2cos2α=cos(α-\frac{π}{4})$,则sin2α的值为( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $-\frac{7}{8}$ | D. | $\frac{7}{8}$ |
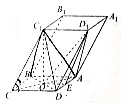 如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.
如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.