题目内容
已知：p：x＜k，q：
≤1，如果p是q的充分不必要条件，则k的取值范围是（ ）
| 3 |
| x+1 |
| A、[2，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（-∞，-1] |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的关系，建立条件关系即可得到结论．
解答：
解：由
≤1得
-1=
=
≤0，解得x≥2或x＜-1，
若p是q的充分不必要条件，
则k≤-1，
故选：D．
| 3 |
| x+1 |
| 3 |
| x+1 |
| 3-x-1 |
| x+1 |
| 2-x |
| x+1 |
若p是q的充分不必要条件，
则k≤-1，
故选：D．
点评：本题主要考查充分条件和必要条件的应用，根据条件求出q的等价条件是解决本题的关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（ ）
A、y=-
| ||
| B、y=lgx | ||
| C、y=cosx | ||
| D、y=e|x| |
将正偶数按下表排成4列：
则2004在（ ）
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 2 | 4 | 6 | 8 |
| 第2行 | 16 | 14 | 12 | 10 |
| 第3行 | 18 | 20 | 22 | 24 |
| … | … | 28 | 26 |
| A、第251行，第1列 |
| B、第251行，第2列 |
| C、第250行，第2列 |
| D、第250行，第4列 |
由下列各组命题构成的复合命题中，“p或q”为真命题，“p且q”为假命题，“非p”为真命题的一组为（ ）
| A、p：3为偶数，q：4为奇数 |
| B、p：π＜3，q：5＞3 |
| C、p：a∈{a，b}，q：{a}?{a，b} |
| D、p：Q?R，q：N=Z |
在三棱锥P-ABC中，AB⊥BC，AB=BC=
PA，点O、D分别是AC、PC的中点，OP⊥底面ABC，则直线OD与平面PBC所成角的正弦值（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
把函数y=cos（x-
）向左平移m（m＞0）个单位，所得的图象关于y轴对称，则m的最小值为（ ）
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
+
的定义域为（ ）
| ||
| x |
| x-2x2 |
A、（
| ||
B、（0，
| ||
C、[0，
| ||
D、[
|
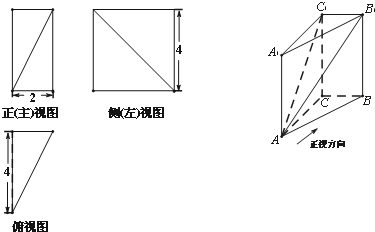某几何体ABC-A1B1C1的三视图和直观图如图所示．