Question

在三棱锥P-ABC中，AB⊥BC，AB=BC=

1

2

PA，点O、D分别是AC、PC的中点，OP⊥底面ABC，则直线OD与平面PBC所成角的正弦值（　　）

• A、

  21

  6

• B、

  8 3

  3

• C、

  210

  60

• D、

  210

  30

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：首先利用三垂线定理作出直线OD与平面PBC所成角，就是取BC中点E，连接PE，则BC⊥平面POE作OF⊥PE于F，连接DF，得到OF⊥平面PBC，然后解三角形求出角即可．

解答： 解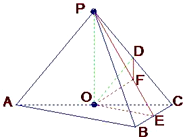：∵AB⊥BC，OA=OC，∴OA=OB=OC，
又∵OP⊥平面ABC
∴PA=PB=PC．取BC中点E，连接PE，则BC⊥平面POE，作OF⊥PE于F，连接DF，则OF⊥平面PBC
∴∠ODF是OD与平面PBC所成的角．设AB=BC=1，PA=2，在Rt△POC中，PO=

14

2

，在Rt△POC中，D是PC的中点，PC=2，
∴OD=1，在Rt△POE中，OE=

1

2

，PE=

15

2

，OF=

PO•OE

PE

=

210

30

，
在Rt△ODF中，sin∠ODF=

OF

OD

=

210

30

故答案为：

210

30

．

点评：本题考查直线与平面所成的角，考查空间想象能力，逻辑思维能力，是中档题．