题目内容
设函数f(x)=|x-a|
(Ⅰ)当a=2,解不等式f(x)≥4-|x-1|;
(Ⅱ)若f(x)≤1的解集为{x|0≤x≤2},
+
=a(m>0,n>0).求证:m+2n≥4.
(Ⅰ)当a=2,解不等式f(x)≥4-|x-1|;
(Ⅱ)若f(x)≤1的解集为{x|0≤x≤2},
| 1 |
| m |
| 1 |
| 2n |
考点:绝对值不等式的解法
专题:不等式
分析:对第(1)问,将a=2代入函数的解析式中,利用分段讨论法解绝对值不等式即可;
对第(2)问,先由已知解集{x|0≤x≤2}确定a值,再将“m+2n”改写为“(m+2n)(
+
)”,展开后利用基本不等式可完成证明.
对第(2)问,先由已知解集{x|0≤x≤2}确定a值,再将“m+2n”改写为“(m+2n)(
| 1 |
| m |
| 1 |
| 2n |
解答:
解:(I)当a=2时,不等式f(x)≥4-|x-1|即为|x-2|≥4-|x-1|,
①当x≤1时,原不等式化为2-x≥4+(x-1),得x≤-
,
故x≤-
;
②当1<x<2时,原不等式化为2-x≥4-(x-1),得2≥5,
故1<x<2不是原不等式的解;
③当x≥2时,原不等式化为x-2≥4-(x-1),得x≥
,
故x≥
.
综合①、②、③知,原不等式的解集为(-∞,-
]∪[
,+∞).
(Ⅱ)证明:由f(x)≤1得|x-a|≤1,从而-1+a≤x≤1+a,
∵f(x)≤1的解集为{x|0≤x≤2},
∴
得a=1,∴
+
=a=1.
又m>0,n>0,∴m+2n=(m+2n)(
+
)=2+(
+
)≥2+2
=4,
当且仅当
=
即m=2n时,等号成立,此时,联立
+
=1,得
时,m+2n=4,
故m+2n≥4,得证.
①当x≤1时,原不等式化为2-x≥4+(x-1),得x≤-
| 1 |
| 2 |
故x≤-
| 1 |
| 2 |
②当1<x<2时,原不等式化为2-x≥4-(x-1),得2≥5,
故1<x<2不是原不等式的解;
③当x≥2时,原不等式化为x-2≥4-(x-1),得x≥
| 7 |
| 2 |
故x≥
| 7 |
| 2 |
综合①、②、③知,原不等式的解集为(-∞,-
| 1 |
| 2 |
| 7 |
| 2 |
(Ⅱ)证明:由f(x)≤1得|x-a|≤1,从而-1+a≤x≤1+a,
∵f(x)≤1的解集为{x|0≤x≤2},
∴
|
| 1 |
| m |
| 1 |
| 2n |
又m>0,n>0,∴m+2n=(m+2n)(
| 1 |
| m |
| 1 |
| 2n |
| 2n |
| m |
| m |
| 2n |
|
当且仅当
| 2n |
| m |
| m |
| 2n |
| 1 |
| m |
| 1 |
| 2n |
|
故m+2n≥4,得证.
点评:1.已知不等式的解集求参数的值,求解的一般思路是:先将原不等式求解一遍,再把结果与已知解集对比即可获得参数的值.
2.本题中,“1”的替换很关键,这是解决此类题型的一种常用技巧,应注意体会证明过程的巧妙性.
2.本题中,“1”的替换很关键,这是解决此类题型的一种常用技巧,应注意体会证明过程的巧妙性.

练习册系列答案
相关题目
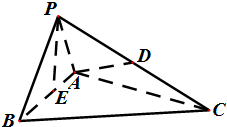 如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=
如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=