题目内容
已知向量
、
和
在正方形网格中的位置如图所示,若
=λ
+μ
,则λ+μ= .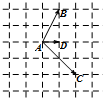
| AC |
| AD |
| AB |
| AC |
| AB |
| AD |

考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:求出向量
、
和
的坐标,进而根据
=λ
+μ
,构造关于λ和μ的方程组,解方程组,求出λ和μ的值,可得答案.
| AC |
| AD |
| AB |
| AC |
| AB |
| AD |
解答:
解:由已知中的图示可得:
=(2,-2),
=(1,0),
=(1,2),
若
=λ
+μ
,
则
,
故λ+μ=2,
故答案为:2
| AC |
| AD |
| AB |
若
| AC |
| AB |
| AD |
则
|
故λ+μ=2,
故答案为:2
点评:本题主要考查平面向量基本定理、两个向量坐标形式的运算,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
设f1(x)=cosx,定义fn+1(x)为fn(x)的导数,即fn+1(x)=f′n(x),n∈N*,若△ABC的内角A满足f1(A)+f2(A)+…+f2014(A)=
,则cos2A的值是 .
| 1 |
| 3 |
已知两不重合直线a、b及两不重合平面α、β,那么下列命题中正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|