题目内容
学校餐厅每天供应500名学生用餐,每星期一有A,B两种菜可供选择.调查表明,凡是在这星期一选A菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有
改选A菜.用an,bn分别表示第n个星期选A的人数和选B的人数.
(1)试用an+1(n∈N*,n≥2)表示an,判断数列{an-300}是否成等比数列并说明理由;
(2)若第一个星期一选A种菜的有200人,那么第10个星期一选A种菜的大约有多少人?
| 1 |
| 5 |
| 3 |
| 10 |
(1)试用an+1(n∈N*,n≥2)表示an,判断数列{an-300}是否成等比数列并说明理由;
(2)若第一个星期一选A种菜的有200人,那么第10个星期一选A种菜的大约有多少人?
考点:数列的应用
专题:应用题,等差数列与等比数列
分析:(1)根据这星期一选A菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有
改选A菜,可得an+1=
an+250,再利用等比数列的定义判断数列{an-300}是否成等比数列;
(2)利用{an-300}是以a1-300为首项,
为公比的等比数列,即可求出第10个星期一选A种菜的人数.
| 1 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
(2)利用{an-300}是以a1-300为首项,
| 1 |
| 2 |
解答:
解:(1)由题知,对n∈N*有bn=500-an,
∴当n∈N*且n≥2时,an=
an-1+
(500-an-1)⇒an=
an-1+250⇒an-300=
(an-1-300),
∴an+1=
an+250,
∴当a1=300时,{an-300}不是等比数列;
当a1≠300时,{an-300}是以a1-300为首项,
为公比的等比数列.
(2)当a1=200时,an-300=(
)n-1(a1-300)⇒an=300-
⇒a10=300-
≈300
∴第10个星期一选A种菜的大约有300人.
∴当n∈N*且n≥2时,an=
| 4 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
∴an+1=
| 1 |
| 2 |
∴当a1=300时,{an-300}不是等比数列;
当a1≠300时,{an-300}是以a1-300为首项,
| 1 |
| 2 |
(2)当a1=200时,an-300=(
| 1 |
| 2 |
| 100 |
| 2n-1 |
| 100 |
| 29 |
∴第10个星期一选A种菜的大约有300人.
点评:本题考查数列知识在生产实际中的应用,理清题设中的数量关系,合理地运用数列知识进行求解是关键.

练习册系列答案
相关题目
执行图(一、12)所示的程序框图,则输出S=( )


| A、112 | B、55 |
| C、110 | D、114 |
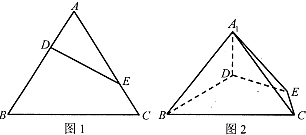
 如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.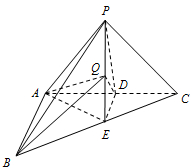 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2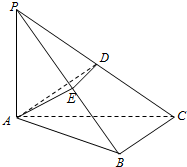 如图,在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2
如图,在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=2