题目内容
证明:
=cot
.
| sinα+sinβ |
| cosα-cosβ |
| β-α |
| 2 |
考点:三角函数恒等式的证明
专题:推理和证明
分析:利用差化积公式,对所证等式的左端的分子与分母变形,约分后,整理可得左端.
解答:
证明:左端=
=-
=
=cot
=右端.
故等式成立.
2sin
| ||||
-2sin
|
cos
| ||
sin
|
cos
| ||
sin
|
| β-α |
| 2 |
故等式成立.
点评:本题考查和差化积公式与诱导公式的应用,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知三棱锥P-ABC,PA⊥面ABC,∠ABC=90°,PA=2,AB=
,BC=1,则该三棱锥的外接球体积为( )
| 3 |
| A、8π | ||||
B、
| ||||
C、
| ||||
D、12
|
下列叙述中正确的是( )
| A、若 p∧(¬q)为假,则一定是p假q真 |
| B、命题“?x∈R,x2≥0”的否定是“?x∈R,x2≥0” |
| C、若a,b,c∈R,则“ab2>cb2”的充分不必要条件是“a>c” |
| D、α是一平面,a,b是两条不同的直线,若 a⊥α,b⊥α,则a∥b |
已知等腰三角形底边的两个端点是A(-1,-1),B(3,7),则第三个顶点C的轨迹方程( )
| A、2x+y-7=0 |
| B、2x+y-7=0(x≠1) |
| C、x+2y-7=0 |
| D、x+2y-7=0(x≠1) |
函数f(x)=log2|2x-1|的图象大致是( )
A、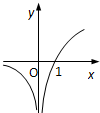 |
B、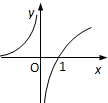 |
C、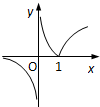 |
D、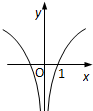 |
设a=(
,1+sinα),b=(1-
,
),且a∥b,则锐角α为( )
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| A、30° | B、45° |
| C、60° | D、75° |