题目内容
已知等腰三角形底边的两个端点是A（-1，-1），B（3，7），则第三个顶点C的轨迹方程（ ）
| A、2x+y-7=0 |
| B、2x+y-7=0（x≠1） |
| C、x+2y-7=0 |
| D、x+2y-7=0（x≠1） |
考点：轨迹方程
专题：计算题,直线与圆
分析：由两点间距离公式得 （x+1）2+（y+1）2=（x-3）2+（y-7）2，化简可得x+2y-7=0，利用A，B，C不共线，即可得出结论．
解答：
解：由两点间距离公式得 （x+1）2+（y+1）2=（x-3）2+（y-7）2，
化简可得x+2y-7=0
∵A，B，C不共线，
∴x≠1且y≠3，
故选：D．
化简可得x+2y-7=0
∵A，B，C不共线，
∴x≠1且y≠3，
故选：D．
点评：本题考查轨迹方程，考查学生的计算能力，容易误选C．
练习册系列答案
相关题目
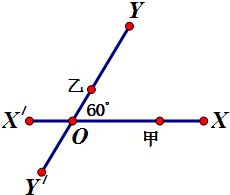如图，有两条相交成60°角的直路XX′，YY′，交点为O，甲、乙分别在OX，OY上，起初甲离O点3km，乙离O点1km，后来甲沿XX′的方向，乙沿Y′Y的方向，同时以4km/h的速度步行．在一次歌咏比赛中，七位裁判为一选手打出的分数如下：
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ ）
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ ）
| A、92，2.8 |
| B、92，2 |
| C、93，2 |
| D、93，2.8 |