题目内容
某工会举办职工猜奖活动,参与者需先后回答A和B两个问题,正确回答问题A可获得奖金m元,正确回答问题B可获得奖金n元(m,n∈N*).活动规定:参与者可任意选择回答的顺序,如果第一个问题回答错误,则该参与者获奖活动中止.现假设职工甲回答问题A答对的概率为
,回答问题B答对的概率为
.
(Ⅰ)求职工甲按先A后B的顺序回答问题获得奖金额的分布列及数学期望;
(Ⅱ)是否存在正整数m和n,使得职工甲不管选择哪种答题顺序所获得奖金额的数学期望一样?若存在,求出m和n的一组值;若不存在,请说明理由.
| 1 |
| 4 |
| 1 |
| 6 |
(Ⅰ)求职工甲按先A后B的顺序回答问题获得奖金额的分布列及数学期望;
(Ⅱ)是否存在正整数m和n,使得职工甲不管选择哪种答题顺序所获得奖金额的数学期望一样?若存在,求出m和n的一组值;若不存在,请说明理由.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)职工甲按先A后B的顺序回答问题获得奖金额X的可能取值为0,m,m+n,分别求出相应的概率,能求出职工甲按先A后B的顺序回答问题获得奖金额的分布列及数学期望.
(Ⅱ)设职工甲先B后A的顺序回答问题获得奖金额为Y,则Y可能取值为0,n,m+n.求出EY,由EX=XY,能求出存在m=120,n=200,使得职工甲不管选择哪种答题顺序所获得奖金额的数学期望一样.
(Ⅱ)设职工甲先B后A的顺序回答问题获得奖金额为Y,则Y可能取值为0,n,m+n.求出EY,由EX=XY,能求出存在m=120,n=200,使得职工甲不管选择哪种答题顺序所获得奖金额的数学期望一样.
解答:
解:(Ⅰ)职工甲按先A后B的顺序回答问题获得奖金额X的可能取值为0,m,m+n,
P(X=0)=
,
P(X=m)=
×
=
,
P(X=m+n)=
×
=
,
∴X的分布列为:
EX=0×
+m×
+(m+n)×
=
.
(Ⅱ)设职工甲先B后A的顺序回答问题获得奖金额为Y,则Y可能取值为0,n,m+n.
P(Y=0)=
,
P(Y=n)=
×
=
,
P(Y=m+n)=
,
Y的分布列为:
EY=0×
+m×
+(m+n)×
=
,
若EX=XY,则6m+n=m+4n,即5m=3n,
∴存在m=120,n=200,使得职工甲不管选择哪种答题顺序所获得奖金额的数学期望一样.
P(X=0)=
| 3 |
| 4 |
P(X=m)=
| 1 |
| 4 |
| 5 |
| 6 |
| 5 |
| 24 |
P(X=m+n)=
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 24 |
∴X的分布列为:
| X | 0 | m | m+n | ||||||
| P |
|
|
|
| 3 |
| 4 |
| 5 |
| 24 |
| 1 |
| 24 |
| 6m+n |
| 24 |
(Ⅱ)设职工甲先B后A的顺序回答问题获得奖金额为Y,则Y可能取值为0,n,m+n.
P(Y=0)=
| 5 |
| 6 |
P(Y=n)=
| 1 |
| 6 |
| 3 |
| 4 |
| 1 |
| 8 |
P(Y=m+n)=
| 1 |
| 24 |
Y的分布列为:
| Y | 0 | m | m+n | ||||||
| P |
|
|
|
| 5 |
| 6 |
| 1 |
| 8 |
| 1 |
| 24 |
| m+4n |
| 24 |
若EX=XY,则6m+n=m+4n,即5m=3n,
∴存在m=120,n=200,使得职工甲不管选择哪种答题顺序所获得奖金额的数学期望一样.
点评:本题考查离散型随机变量的分布列和数学期望的求法及其应用,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
相关题目
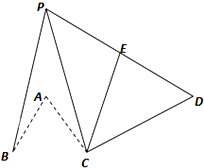 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.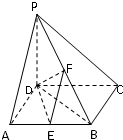 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.