题目内容
△ABC中，AC=
，BC=
，∠B=60°，则∠A= ．
| 3 |
| 2 |
考点：正弦定理
专题：计算题,解三角形
分析：由已知及正弦定理可得sinA=
，又AC=
＞BC=
，由大边对大角即可求∠A．
| ||
| 2 |
| 3 |
| 2 |
解答：
解：∵由正弦定理可得：sinA=
=
=
，
又∵AC=
＞BC=
，
∴∠B=60°＞∠A，
∴∠A=
．
故答案为：
．
| BC×sinB |
| AC |
| ||
|
| ||
| 2 |
又∵AC=
| 3 |
| 2 |
∴∠B=60°＞∠A，
∴∠A=
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题主要考查了正弦定理、大边对大角等知识的应用，属于基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知圆C：x2+y2-2x+4y+1=0，在区间[-4，6]上任取整数m，则直线l：x+y+m=0与圆C相交所得△ABC为钝角三角形（其中A、B为交点，C为圆心）的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数 f（x）=sin（ωx+φ）+b的图象如图，则 f（x）的解析式S=f（1）+f（2）+f（3）+…+f（2015）的值分别为（ ）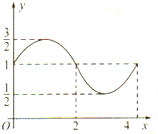
A、f（x）=
| ||||||
B、f（x）=
| ||||||
C、f（x）=
| ||||||
D、f（x）=
|
如图，在一个边长为2的正方形中有一封闭的“★”型阴影区域，向正方形中随机撒入200粒豆子，若恰有40粒落在阴影区域内，则该阴影部分的面积约为（ ）函数f（x）满足f（x+2）=f（x），且在x∈[0，2）时，f（x）=
，若直线kx-y+k=0（k＞0）与函数f（x）的图象有且仅有三个不同交点，则k的取值范围是（ ）
| 2x-x2 |
A、(
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|