题目内容
已知两点A(-1,0),B(-1,
).O为坐标原点,点C在第一象限,且∠AOC=120°,设
=-3
+λ
(λ∈R),则λ= .
| 3 |
| OC |
| OA |
| OB |
考点:向量加减混合运算及其几何意义
专题:平面向量及应用
分析:先根据题意及向量加法的平行四边形法则,作出向量
,找出表示
的两基向量,由A(-1,0),B(-1,
)得∠AOB=60°,再利用∠AOC=120°可得平行四边形的特征,从而得到|
|,最后利用向量数量积的计算公式获得λ的值.
| OC |
| OC |
| 3 |
| OC |
解答:
解:如右图所示,作向量
=-3
=(3,0),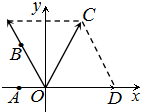
则
=-3
+λ
=
+λ
,
∵点C在第一象限,点B的坐标为(-1,
),∴∠OCD=∠AOB=60°,
又∵∠AOC=120°,∴∠COD=60°,
∴△COD为正三角形,∴|
|=|
|=3,
∵
=(3,0)+λ(-1,
)=(3-λ,
λ),
∴cos∠AOC=
=
,
即cos120°=
=-
,得λ=
.
故答案为:
.
| OD |
| OA |

则
| OC |
| OA |
| OB |
| OD |
| OB |
∵点C在第一象限,点B的坐标为(-1,
| 3 |
又∵∠AOC=120°,∴∠COD=60°,
∴△COD为正三角形,∴|
| OC |
| OD |
∵
| OC |
| 3 |
| 3 |
∴cos∠AOC=
| ||||
|
|
(-1,0)•(3-λ,
| ||
| 1×3 |
即cos120°=
| λ-3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:1.本题考查了向量加法的平行四边形法则,平面向量基本定理及数量积的运算等,关键是如何作出和向量
及加向量λ
.
2.当然本题中求得|
|=3后,还可根据向量的模长公式列出关于λ的一元二次方程,从而可求得λ的值,应注意根的取舍.
| OC |
| OB |
2.当然本题中求得|
| OC |

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
设数列{an}是首项为1,公比为q(q≠-1)的等比数列,若{
}是等差数列,则(
+
)+(
+
)+…+(
+
)=( )
| 1 |
| an+an+1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2013 |
| 1 |
| a2014 |
| A、2012 | B、2013 |
| C、4024 | D、4026 |
 如图所示,在平行四边形ABCD中,E是BC的中点,G为AC与DE的交点,若
如图所示,在平行四边形ABCD中,E是BC的中点,G为AC与DE的交点,若