题目内容
已知向量
=(1,2sinθ),
=(sin(θ+
),1),θ∈R.
(1)若
⊥
,求tanθ的值;
(2)若
∥
,且θ∈(0,
),求θ的值.
| a |
| b |
| π |
| 3 |
(1)若
| a |
| b |
(2)若
| a |
| b |
| π |
| 2 |
考点:平面向量共线(平行)的坐标表示,平面向量数量积的运算
专题:平面向量及应用
分析:由向量的垂直和平行的性质得到θ的三角函数式,然后化简解答.
解答:
解;(1)若
⊥
,则
•
=sin(θ+
)+2sinθ=0,所以5sinθ+
cosθ=0,所以tanθ=-
;
(2)若
∥
,且θ∈(0,
),则2sinθsin(θ+
)=1,整理得sin2θ+
sinθcosθ=1,所以
+
sin2θ=1,所以
sin2θ-
cos2θ=
,即sin(2θ-
)=
,θ∈(0,
),2θ-
∈(-
,
),所以2θ-
=
,所以θ=
.
| a |
| b |
| a |
| b |
| π |
| 3 |
| 3 |
| ||
| 5 |
(2)若
| a |
| b |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 1-cos2θ |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
点评:本题考查了向量的垂直和平行的性质以及运用三角函数公式化简三角函数并求值.

练习册系列答案
相关题目
设
(x+1)k=a0+a1x+a2x2+a3x3+…+a100x
,则
=( )
| 100 |
 |
| k=1 |
| 100 |
| a4 |
| a5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
点P(x,y)在不等式组
表示的平面区域内,若点P(x,y)到直线y=kx-1的最大距离为2
,则k为( )
|
| 2 |
| A、-1 | B、-1或1 |
| C、-1或2 | D、1 |
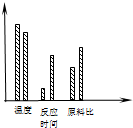 如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )
如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )| A、影响试验结果最主要的因素是温度 |
| B、影响试验结果最主要的因素是反应时间 |
| C、影响试验结果最主要的因素是原料比 |
| D、因图中数据不全,无法分清哪个因素影响最大 |