题目内容
6.关于x的方程$x={log_a}(-{x^2}+2x+a)$(a>0,且a≠1)解的个数是( )| A. | 2 | B. | 1 | C. | 0 | D. | 不确定的 |
分析 由题意ax=-x2+2x+a,-x2+2x+a>0,令f(x)=ax,g(x)=-x2+2x+a,分类讨论,即可得出结论.
解答 解:由题意ax=-x2+2x+a,-x2+2x+a>0.
令f(x)=ax,g(x)=-x2+2x+a,
(1)当a>1时,
f(x)=ax在(-∞,+∞)上单调递增,且f(0)=1,f(1)=a,
g(x)=-x2+2x+a在[0,1]上单调递增,在[1,+∞)上单调递减,且g(0)=a,g(1)=1+a,
在[0,1]上,f(x)<g(x),
∵g(x)在x<0及x>1时分别有一个零点,而f(x)恒大于零,
∴f(x)与g(x)的图象在x<0及x>1时分别有一个交点,
∴方程有两个解;
(2)当a<1时,
f(x)=ax在(-∞,+∞)上单调递减,且f(0)=1,f(1)=a,
g(x)=-x2+2x+a在[0,1]上单调递增,在[1,+∞)上单调递减,且g(0)=a,g(1)=1+a,
f(0)>g(0),f(1)<g(1),
∴在(0,1)上f(x)与g(x)有一个交点,
又g(x)在x>1时有一个零点,而f(x)恒大于零,
∴f(x)与g(x)的图象在x>1时还有一个交点,
∴方程有两个解.
综上所述,方程有两个解.
故选:A.
点评 本题考查根的存在性及个数的判断,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.已知正△ABC内接于半径为2的圆O,点P是圆O上的一个动点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是( )
| A. | [0,6] | B. | [-2,6] | C. | [0,2] | D. | [-2,2] |
11.计算:4cos50°-tan40°=( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
18.命题“?x0∈(0,+∞),lnx0=2x0+1”的否定是( )
| A. | ?x0∈(0,+∞),lnx0≠2x0+1 | B. | ?x0∉(0,+∞),lnx0=2x0+1 | ||
| C. | ?x∈(0,+∞),lnx≠2x+1 | D. | ?x∉(0,+∞),lnx≠2x+1 |
15.已知△ABC的两个顶点A(5,0),B(-5,0),周长为22,则顶点C的轨迹方程是( )
| A. | $\frac{x^2}{36}+\frac{y^2}{11}=1$ | B. | $\frac{x^2}{36}+\frac{y^2}{11}=1({y≠0})$ | ||
| C. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{16}=1({y≠0})$ |
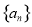 满足
满足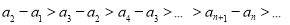 ,则称数列
,则称数列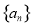 为“差递减”数列.若数列
为“差递减”数列.若数列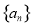 是“差递减”数列,且其通项
是“差递减”数列,且其通项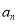 与其前
与其前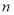 项和
项和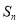 (
( )满足
)满足 (
(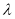 的取值范围是 .
的取值范围是 .