题目内容
“x=kπ+
（k∈Z）“是“tanx=1”成立的（ ）
| π |
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据三角函数，充分必要条件的定义判断．
解答：
解：∵tanx=1，∴x=kπ+
（k∈Z）
∵x=kπ+
（k∈Z）则tanx=1，
∴根据充分必要条件定义可判断：
“x=kπ+
（k∈Z）“是“tanx=1”成立的充分必要条件
故选：C
| π |
| 4 |
∵x=kπ+
| π |
| 4 |
∴根据充分必要条件定义可判断：
“x=kπ+
| π |
| 4 |
故选：C
点评：本题考察了充分必要条件的定义，属于容易题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
i是虚数单位，复数（1-i）2的虚部为（ ）
| A、-2 | B、2 | C、-2i | D、2i |
直线x+
y=0被圆x2+y2-4y=0所截得的弦长为（ ）
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
设a=log23，b=log43，c=（
）12，则它们的大小关系是（ ）
| 1 |
| 2 |
| A、c＜a＜b |
| B、b＜c＜a |
| C、b＜a＜c |
| D、c＜b＜a |
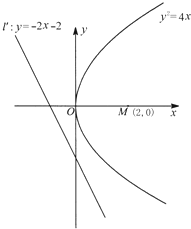过点M（2，0）的直线l与抛物线C：y2=4x相交于A，B两点，过点A，B分别作y轴的垂线交直线l′：y=-2x-2于点A′，B′．