题目内容
（文做）已知函数f（x）=x2-k（x+1）+x的一个零点在（2，3）内，求实数k的取值范围．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：根据函数的零点的判断方法，求解，列出不等式，求解不等根即可．
解答：
解：∵函数f（x）=x2+（1-k）x-k，
∴△=（1-k）2+4k=（1+k）2≥0，函数f（x）=x2-k（x+1）+x的有零点
（1）当k=-1时，f（x）的零点有1个，为-1，
∴零点不在（2，3）内，
（2）当k≠-1时，f（x）的零点有2个，
∵函数f（x）=x2-k（x+1）+x的一个零点在（2，3）内
∴f（2）f（3）＜0，
即（6-3k）（12-4k）＜0
（k-2）（k-3）＜0，
∴2＜k＜3
故实数k的取值范围为：（2，3）
∴△=（1-k）2+4k=（1+k）2≥0，函数f（x）=x2-k（x+1）+x的有零点
（1）当k=-1时，f（x）的零点有1个，为-1，
∴零点不在（2，3）内，
（2）当k≠-1时，f（x）的零点有2个，
∵函数f（x）=x2-k（x+1）+x的一个零点在（2，3）内
∴f（2）f（3）＜0，
即（6-3k）（12-4k）＜0
（k-2）（k-3）＜0，
∴2＜k＜3
故实数k的取值范围为：（2，3）
点评：本题考查了函数零点的判定定理，解不等式，属于容易题．
练习册系列答案
相关题目
直线x+
y=0被圆x2+y2-4y=0所截得的弦长为（ ）
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
已知
，
是平面上的两个不共线向量，向量
=2
-
，
=m
+3
．若
∥
，则实数m=（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
| A、6 | ||
| B、-6 | ||
| C、3 | ||
D、
|
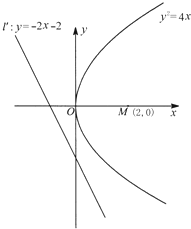过点M（2，0）的直线l与抛物线C：y2=4x相交于A，B两点，过点A，B分别作y轴的垂线交直线l′：y=-2x-2于点A′，B′．
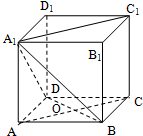如图，在棱长为a的正方体 ABCD-A1B1C1D1 中，AC 与BD相交于点O．