题目内容
已知在△ABC中,a,b,c分别是角A,B,C的对边,a=2sinA且
=-
(Ⅰ)求角B的大小;
(Ⅱ)求△ABC面积的最大值.
| cosB |
| cosC |
| b |
| 2a+c |
(Ⅰ)求角B的大小;
(Ⅱ)求△ABC面积的最大值.
考点:余弦定理的应用,正弦定理的应用
专题:解三角形
分析:(Ⅰ)由正弦定理原式可化简为2sinAcosB+sinA=0,因为sinA≠0,故cosB=-
,即可求出B的值;
(Ⅱ)由正弦定理可求b=
,而b2=a2+c2+ac≥3ac.故有ac≤1,从而可求△ABC面积的最大值.
| 1 |
| 2 |
(Ⅱ)由正弦定理可求b=
| 3 |
解答:
解:(Ⅰ)由正弦定理,得
=-
,
即2sinAcosB+sinCcosB+cosCsinB=0,即2sinAcosB+sin(B+C)=0
又A+B+C=π,所以sin(B+C)=sinA,
故2sinAcosB+sinA=0,因为sinA≠0,故cosB=-
,
又因为B为三角形的内角,所以B=
.
(Ⅱ)因为
=
=
=2,
所以b=
,而b2=a2+c2+ac≥3ac.
故有ac≤1,
所以S=
acsinB≤
.
| cosB |
| cosC |
| sinB |
| 2sinA+sinC |
即2sinAcosB+sinCcosB+cosCsinB=0,即2sinAcosB+sin(B+C)=0
又A+B+C=π,所以sin(B+C)=sinA,
故2sinAcosB+sinA=0,因为sinA≠0,故cosB=-
| 1 |
| 2 |
又因为B为三角形的内角,所以B=
| 2π |
| 3 |
(Ⅱ)因为
| a |
| sinA |
| b |
| sinB |
| 2b | ||
|
所以b=
| 3 |
故有ac≤1,
所以S=
| 1 |
| 2 |
| ||
| 4 |
点评:本题主要考察了余弦定理、正弦定理的综合应用,所以中档题.

练习册系列答案
相关题目
在空间中,下列命题正确的是( )
| A、三条直线两两相交,则这三条直线确定一个平面 |
| B、若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β |
| C、若直线m与平面α内的一条直线平行,则m∥α |
| D、若直线a与直线b平行,且直线l⊥a,则l∥b |
设F1,F2是椭圆
+
=1的两焦点,M为椭圆上的点,若MF1⊥MF2,则△MF1F2的面积为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、4 | ||
| B、8 | ||
C、4
| ||
D、8
|
 函数y=f(x)在定义域(-3,5)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域(-3,5)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、(-3,-1]∪[
| ||
B、[-
| ||
C、[-1 ,
| ||
D、(-3 , -
|
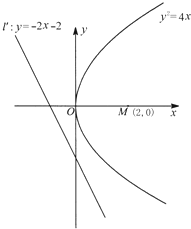 过点M(2,0)的直线l与抛物线C:y2=4x相交于A,B两点,过点A,B分别作y轴的垂线交直线l′:y=-2x-2于点A′,B′.
过点M(2,0)的直线l与抛物线C:y2=4x相交于A,B两点,过点A,B分别作y轴的垂线交直线l′:y=-2x-2于点A′,B′.