题目内容
18. 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=AP,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=AP,PA⊥底面ABCD,E是PC的中点.(1)求证:BE∥平面PAD;
(2)求异面直线PD与BC所成角的余弦值.
分析 (1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明BE∥平面PAD.
(2)求出$\overrightarrow{PD}$=(0,2,-2),$\overrightarrow{BC}$=(1,2,0),由此利用向量法能求出异面直线PD与BC所成角的余弦值.
解答 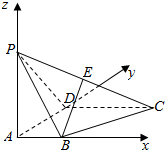 证明:(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
证明:(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
设CD=AD=2AB=AP=2,
则B(1,0,0),P(0,0,2),C(2,2,0),E(1,1,1),
$\overrightarrow{BE}$=(0,1,1),
∵平面PAD的法向量$\overrightarrow{n}$=(1,0,0),∴$\overrightarrow{BE}•\overrightarrow{n}$=0,
∵BE?平面PAD,∴BE∥平面PAD.
解:(2)D(0,2,0),$\overrightarrow{PD}$=(0,2,-2),$\overrightarrow{BC}$=(1,2,0),
设异面直线PD与BC所成角为θ,
则cosθ=$\frac{|\overrightarrow{PD}•\overrightarrow{BC}|}{|\overrightarrow{PD}|•|\overrightarrow{BC}|}$=$\frac{|4|}{\sqrt{8}•\sqrt{5}}$=$\frac{\sqrt{10}}{5}$,
所以异面直线PD与BC所成角的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查线面平行的证明,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
9.“$\frac{1}{a}$>$\frac{1}{b}$”是“a<b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.以下命题中错误的是( )
| A. | 若直线与平面没有公共点,则它们平行 | |
| B. | 如果两直线没有公共点,那么这两直线平行 | |
| C. | 若两平面没有公共点,则它们平行 | |
| D. | 若一个平面经过另一个平面的一条垂线,则这两个平面垂直 |
8.函数f(x)=3-2sin2x是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
 的值域是__________.
的值域是__________.