题目内容
3.已知0<α<$\frac{π}{2}$,sinα=$\frac{4}{5}$.(1)求tanα的值;
(2)求cosα+sin(α+$\frac{π}{2}$)的值.
分析 (1)利用同角三角函数关系式求解.
(2)利用诱导公式求解.
解答 解:(1)∵0<α<$\frac{π}{2}$,sinα=$\frac{4}{5}$,
∴cosα=$\sqrt{1-(\frac{4}{5})^{2}}$=$\frac{3}{5}$,
∴tanα=$\frac{sinα}{cosα}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}$.
(2)cosα+sin(α+$\frac{π}{2}$)
=cosα+cosα
=2cosα
=$\frac{6}{5}$.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意同角三角函数关系式和诱导公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若在△ABC中,∠A=30°,b=3,S△ABC=$\sqrt{3}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=( )
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{21}}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $13\sqrt{2}$ |
8.定义在R的奇函数f(x),当x<0时,f(x)=-x2+x,则x>0时,f(x)等于( )
| A. | x2+x | B. | -x2+x | C. | -x2-x | D. | x2-x |
 ,则要得到其导函数
,则要得到其导函数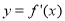 的图象,只需将函数
的图象,只需将函数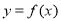 的图象( )
的图象( )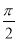 个单位
个单位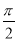 个单位
个单位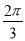 个单位
个单位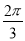 个单位
个单位 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=AP,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=AP,PA⊥底面ABCD,E是PC的中点.