题目内容
19.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且满足2acosC=2b-$\sqrt{3}$c.(1)求角A;
(2)若B=$\frac{π}{6}$,且BC边上的中线AM的长为$\sqrt{7}$,求此时△ABC的面积.
分析 (1)△ABC中,由条件利用正弦定理可得2cosAsinC=$\sqrt{3}$sinC,化简可得cosA=$\frac{\sqrt{3}}{2}$,由此求得A的值.
(2)设等腰三角形腰长为x,即AC=BC=x,CM=$\frac{1}{2}$x,在三角形ACM中,利用余弦定理列出关于x的方程,求出方程的解得到x的值,确定出AC与BC的长,再利用三角形面积公式即可求出三角形ABC面积.
解答 (本题满分为12分)
解:(1)△ABC中,∵2acosC=2b-$\sqrt{3}$c.
∴由正弦定理得:2sinB-$\sqrt{3}$sinC=2sinAcosC,------(2分)
∵2sinB=2sin(A+C)=2sinAcosC+2cosAsinC,
∴化简可得:2cosAsinC=$\sqrt{3}$sinC,---------(4分)
∵sinC≠0,
∴cosA=$\frac{\sqrt{3}}{2}$,
∴由A∈(0,π),可得:A=$\frac{π}{6}$.---------(6分)
(2)设等腰三角形腰长为x,即AC=BC=x,CM=$\frac{1}{2}$x,
在△ACM中,由余弦定理得:AM2=AC2+CM2-2AC•CM•cosC,即7=x2+$\frac{1}{4}$x2+$\frac{1}{2}$x2,
解得:x=2,
则S△ABC=$\frac{1}{2}$AC•BC•sinC=$\sqrt{3}$.---------(12分)
点评 此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理是解本题的关键,属于基础题.

练习册系列答案
相关题目
9.下列各式运算错误的是( )
| A. | (-a2b)2•(-ab2)3=-a7b8 | B. | [-(a3)2•(-b2)3]3=a18b18 | ||
| C. | (-a3)2•(-b2)3=a6b6 | D. | (-a2b3)3÷(-ab2)3=a3b3 |
10.已知函数f(x)=2x2,则f′(1)等于( )
| A. | 4 | B. | 2 | C. | 4+2△x | D. | 4+2(△x)2 |
7.如图所示的算法流程图中,若f(x)=sinx,g(x)=tanx,$h(-\frac{π}{6})$的值等( )
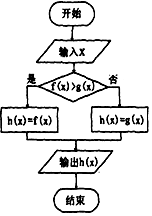

| A. | -$\frac{{\sqrt{3}}}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
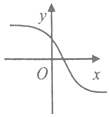
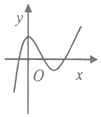
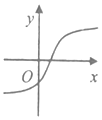
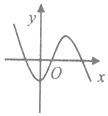
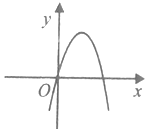 已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )
已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )