题目内容
14.在△ABC中,内角A,B,C的对边分别为a,b,c,已知$\frac{3c-a}{b}$=$\frac{cosA-3cosC}{cosB}$.(1)求$\frac{sinA}{sinC}$的值;
(2)若B为钝角,b=10,求a的取值范围.
分析 (1)利用正弦定理、和差公式即可得出.
(2)由(1)及正弦定理知$\frac{a}{c}=\frac{1}{3}$,即c=3a.由题意:$\left\{\begin{array}{l}{b=10}\\{a+c>b}\\{{a}^{2}+{c}^{2}<{b}^{2}}\end{array}\right.$,解之即可得出.
解答 解:(1)由正弦定理:设$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=k,又$\frac{3c-a}{b}$=$\frac{cosA-3cosC}{cosB}$.
∴$\frac{3sinC-sinA}{sinB}$=$\frac{cosA-3cosC}{cosB}$.
化为:(cosA-3cosC)sinB=(3sinC-sinA)cosB,
化简得:cosAsinB+sinAcosB=3(sinBcosC+cosBsinC),即sin(A+B)=3sin(B+C),
∴sinC=3sinA,即$\frac{sinA}{sinC}$=$\frac{1}{3}$.
(2)由(1)及正弦定理知$\frac{a}{c}=\frac{1}{3}$,即c=3a.
由题意:$\left\{\begin{array}{l}{b=10}\\{a+c>b}\\{{a}^{2}+{c}^{2}<{b}^{2}}\end{array}\right.$,解之得:$\frac{5}{2}<a<\sqrt{10}$,
则a的取值范围是$(\frac{5}{2},\sqrt{10})$.
点评 本题考查了正弦定理余弦定理、和差公式、三角形三边大小关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若x>0,y>0,且$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$,则xy有( )
| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
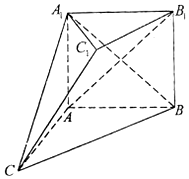 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC