题目内容
3.$若f(n)=tan\frac{nπ}{3},(n∈{N^*}),则f(1)+f(2)+…+f(100)$=( )| A. | $-\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | 0 | D. | $\sqrt{3}$ |
分析 根据正切函数的性质可得其周期T=$\frac{π}{\frac{π}{3}}=3$,依次求出f(1),f(2),f(3),由周期可得f(1)+f(2)+…+f(100)的值.
解答 解:∵f(n)=$tan\frac{nπ}{3}$,
根据正切函数的性质可得其周期T=$\frac{π}{\frac{π}{3}}=3$,
∴f(1)=$\sqrt{3}$,f(2)=$-\sqrt{3}$,f(3)=0.
可得:f(1)=f(2)+f(3)=0.
∴f(1)+f(2)+…+f(100)=33[f(1)+f(2)+f(3)]+f(1)=f(1)=$\sqrt{3}$.
故选:D.
点评 本题主要考查正切函数的图象和性质,周期函数的求和计算.属于基础题

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
13. 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有平面A′GF⊥平面BCED | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
11.已知角α的终边与单位圆交于点$P(-\frac{{\sqrt{3}}}{2},-\frac{1}{2})$,则cosα的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
8.定义在实数域上的偶函数f(x)对于?x∈R,均满足条件f(x+2)=f(x)+f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)在(0,+∞)上至少有5个零点,则a的取值范围是( )
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{3}}{3}$) | C. | (0,$\frac{\sqrt{5}}{5}$) | D. | (0,$\frac{\sqrt{6}}{6}$) |
15.已知集合A={x|x>-1},B={x|x2+2x-3<0}则A∩B=( )
| A. | (-1,3) | B. | (-1,1) | C. | (-1,+∞) | D. | (-3,1) |
9.某城市理论预测2000年到2004年人口总数与年份的关系如表所示
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)此次估计2005年该城市人口总数.
(参考公式:用最小二乘法求线性回归方程系数的公式:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(2)此次估计2005年该城市人口总数.
(参考公式:用最小二乘法求线性回归方程系数的公式:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
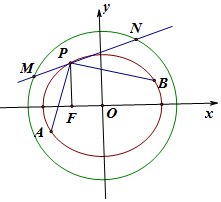 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).