题目内容
15．
有一些正整数排成的倒三角，从第二行起，每个数字等于“两肩”数的和，最后一行只有一个数M，那么M=576．
分析 从第一行为1，2和1，2，3 和1，2，3，4的两个“小三角形”入手，结合图形归纳得出结果，猜测出M
解答 解：若第一行为1，2，则M=3=（2+1）×22-2；
若第一行为1，2，3，则M=8=（3+1）×23-2；
若第一行为1，2，3，4，则M=20=（4+1）×24-2；
…
归纳可得：若第一行为1，2，3，4，…，n，则M=（n+1）×2n-2．
当n=8时，M=9×26=576，
故答案为：576
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
相关题目
18．在△ABC中，若a=1，A=60°，B=45°，则b=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{6}}}{2}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
3．已知数列{an}为等比数列，若a7=$\frac{5}{2}$，公比q=2${\;}^{\frac{1}{5}}$，则a3（a1+2a11+a21）的值为（ ）
| A． | 36 | B． | 6 | C． | $\frac{625}{16}$ | D． | $\frac{25}{4}$ |
10．执行如图所示的程序框图，若输入x=0，输出K的值为10，则判断框内可填入的条件是（ ）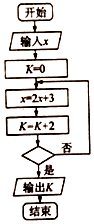
| A． | x＞50？ | B． | x＞90？ | C． | x＞100？ | D． | x＞200？ |
20．在区间[0，π]上随机取一个数，使函数y=cosx的函数值落在$[-\frac{{\sqrt{3}}}{2}，\frac{{\sqrt{3}}}{2}]$上的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{3}}}{4}$ |
7．设等差数列{an}的前n项和为Sn，且S2016＞0，S2017＜0，则当Sn最大时的序号n为（ ）
| A． | 1007 | B． | 1008 | C． | 1009 | D． | 2016 |