题目内容
已知a>0且a≠1,若函数f(x)=
,在[-2,2]的最大值为2,则f[f(-1)]= ,a= .
|
考点:分段函数的应用
专题:计算题,分类讨论,函数的性质及应用
分析:对a讨论,a>1,0<a<1时,由指数函数和对数函数的单调性可得最值,判断a>1不成立,计算即可得到a,再求f(-1),进而得到f[f(-1)].
解答:
解:当a>1时,y=ax+1在[-2,1)递增,无最大值,
y=log2x在[1,2]上递增,则最大值为log22=1,
与题意不符,则舍去;
当0<a<1时,y=ax+1在[-2,1)上递减,则最大值为a-1=2,
即a=
,f(-1)=(
)0=1,
f[f(-1)]=f(1)=log21=0,
故答案为:0,
.
y=log2x在[1,2]上递增,则最大值为log22=1,
与题意不符,则舍去;
当0<a<1时,y=ax+1在[-2,1)上递减,则最大值为a-1=2,
即a=
| 1 |
| 2 |
| 1 |
| 2 |
f[f(-1)]=f(1)=log21=0,
故答案为:0,
| 1 |
| 2 |
点评:本题考查分段函数的运用:求函数值,考查指数函数和对数函数的单调性的运用,考查分类讨论的思想方法,考查运算能力,属于中档题和易错题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
已知函数f(x)=sinx+cosx,x∈R,则下列结论正确的是( )
| A、f(x)是奇函数 | ||
| B、f(x)的值域为[-2,2] | ||
C、f(x)关于点(-
| ||
D、f(x)有一条对称轴为x=
|
函数f(x)的导函数f′(x)的图象如图所示,则下列说法正确的是( )
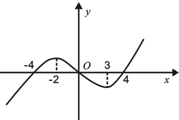

| A、函数f(x)在(-2,3)内单调递减 |
| B、函数f(x)在x=3处取极小值 |
| C、函数f(x)在(-4,0)内单调递增 |
| D、函数f(x)在x=4处取极大值 |
下列结论正确的是( )
A、x>1⇒
| ||||
B、x+
| ||||
C、x>y⇒
| ||||
| D、x>y⇒x2>y2 |