题目内容
函数f（x）的导函数f′（x）的图象如图所示，则下列说法正确的是（ ）
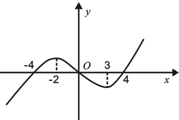
| A、函数f（x）在（-2，3）内单调递减 |
| B、函数f（x）在x=3处取极小值 |
| C、函数f（x）在（-4，0）内单调递增 |
| D、函数f（x）在x=4处取极大值 |
考点：函数图象的作法,函数的图象
专题：导数的综合应用
分析：直接利用导函数的图象的值域，判断函数的单调性即可．
解答：
解：函数f（x）的导函数f′（x）的图象如图所示，
可得x∈（-4，0），f′（x）＞0，函数是增函数．x∈（0，4），f′（x）＜0，函数是减函数．
x=4时，f′（4）=0，函数取得极小值，
所以选项C正确．
故选：C．
解：函数f（x）的导函数f′（x）的图象如图所示，可得x∈（-4，0），f′（x）＞0，函数是增函数．x∈（0，4），f′（x）＜0，函数是减函数．
x=4时，f′（4）=0，函数取得极小值，
所以选项C正确．
故选：C．
点评：本题考查函数的导数以及函数的图象的应用，考查基本知识的应用．
练习册系列答案
阅读快车系列答案
相关题目
函数y=
sin（x-
）得图象的一条对称轴是直线（ ）
| 1 |
| 2 |
| π |
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
已知函数f（x）=sin2x（x∈R），为了得到函数g（x）=sin（2x+
）的图象，只要将y=f（x）的图象（ ）
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
设α，β都是锐角，且cosα=
，sin（α-β）=
，则cosβ=（ ）
| ||
| 5 |
| ||
| 10 |
A、
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|