题目内容
12.已知数列{an}为等差数列,a4+a9=24,a6=11,则a7=13.分析 利用等差数列通项公式列出方程组,求出首项和公差,由此能求出a7.
解答 解:∵数列{an}为等差数列,a4+a9=24,a6=11,
∴$\left\{\begin{array}{l}{{a}_{1}+3d+{a}_{1}+8d=24}\\{{a}_{1}+5d=11}\end{array}\right.$,
解得a1=1,d=2,
∴a7=a1+6d=1+12=13.
故答案为:13.
点评 本题考查等差数列的第7项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
4.定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}$|=ad-bc,则符合条件$|{\begin{array}{l}z&{1+2i}\\{1-2i}&{1-i}\end{array}}$|=0的复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知点P是直线l:3x-y-2=0上任意一点,过点P引圆(x+3)2+(y+1)2=1的切线,则切线长度的最小值为( )
| A. | 3 | B. | $\sqrt{7}$ | C. | 2 | D. | 1 |
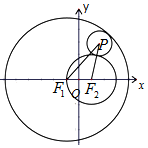 已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.
已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.