题目内容
8.设角α的终边经过点(2$\sqrt{2}$,-1),则sinα=-$\frac{1}{3}$.分析 由角α的终边经过点(2$\sqrt{2}$,-1),利用任意角的三角函数定义求出sinα即可.
解答 解:∵角α的终边经过点(2$\sqrt{2}$,-1),
∴x=2$\sqrt{2}$,y=-1,
∴r=$\sqrt{{x}^{2}+{y}^{\;}}$=3,
∴sinα=$\frac{y}{r}$=-$\frac{1}{3}$,
故答案为:-$\frac{1}{3}$.
点评 此题考查了任意角的三角函数定义,熟练掌握三角函数的定义是解本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13.容量为20的样本数据,分组后的频数如表:
则样本数据落在区间[10,40)的频率为0.45.
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
20.已知点P是直线l:3x-y-2=0上任意一点,过点P引圆(x+3)2+(y+1)2=1的切线,则切线长度的最小值为( )
| A. | 3 | B. | $\sqrt{7}$ | C. | 2 | D. | 1 |
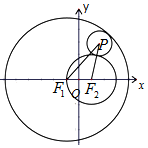 已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.
已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.