题目内容
3.若数列{an}满足:a1=0,且an=an-1+2n-1(n∈N*,n≥2),数列{bn}满足bn=$\sqrt{{a}_{n}+1}$•$\sqrt{{a}_{n+1}+1}$•($\frac{8}{11}$)n-1,则数列{bn}的最大项为第6项.分析 由已知数列递推式利用累加法求得数列{an}的通项公式,代入bn=$\sqrt{{a}_{n}+1}$•$\sqrt{{a}_{n+1}+1}$•($\frac{8}{11}$)n-1,整理后利用$\left\{\begin{array}{l}{{b}_{n}≥{b}_{n-1}}\\{{b}_{n}≥{b}_{n+1}}\end{array}\right.$求解关于n的不等式组得答案.
解答 解:由a1=0,且an=an-1+2n-1(n∈N*,n≥2),
得an-an-1=2n-1(n≥2),则
a2-a1=2×2-1,
a3-a2=2×3-1,
a4-a3=2×4-1,
…
an=an-1+2n-1(n≥2),
累加得:an=2(2+3+…+n)-(n-1)=$2×\frac{(n+2)(n-1)}{2}-n+1$=n2-1.
∴bn=$\sqrt{{a}_{n}+1}$•$\sqrt{{a}_{n+1}+1}$•($\frac{8}{11}$)n-1 =$\sqrt{{n}^{2}}•\sqrt{(n+1)^{2}}•(\frac{8}{11})^{n-1}$=$({n}^{2}+n)•(\frac{8}{11})^{n-1}$.
由$\left\{\begin{array}{l}{{b}_{n}≥{b}_{n-1}}\\{{b}_{n}≥{b}_{n+1}}\end{array}\right.$,得$\left\{\begin{array}{l}{({n}^{2}+n)•(\frac{8}{11})^{n-1}≥({n}^{2}-n)•(\frac{8}{11})^{n-2}}\\{({n}^{2}+n)•(\frac{8}{11})^{n-1}≥({n}^{2}+3n+2)•(\frac{8}{11})^{n}}\end{array}\right.$,
即$\frac{16}{3}≤n≤\frac{19}{3}$,
∵n∈N*,∴n=6.
∴数列{bn}的最大项为第6项.
故答案为:6.
点评 本题考查数列递推式,训练了累加法求数列的通项公式,根据条件建立不等式组是解决本题的关键,是中档题.

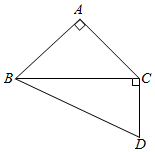 如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.