题目内容
14.已知函数f(x)的定义域是R,对任意实数x,满足f(x+2)=-f(x),求证:函数f(x)是周期函数.分析 根据函数周期的定义进行证明即可.
解答 证明:∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),
即函数f(x)是周期为4的周期函数.
点评 本题主要考查函数周期的证明,根据周期函数的定义是解决本题的关键.比较基础.

练习册系列答案
相关题目
2.已知an是二项式(2+$\sqrt{x}$)n(其中n=2,3,4,…)的展开式中x的二项式系数,若数列{bn}满足b1=160,bn=$\frac{2{a}_{n+2}{a}_{n+3}}{(n+2){a}_{n+1}}$(n≥2,n∈N*),则数列{bn}的最小项是( )
| A. | 40 | B. | 10 | C. | 160 | D. | 320 |
9.从某校的一次学料知识竞赛成绩中,随机抽取了50名同学的成绩,统计如下:
(Ⅰ)求这50名同学成绩的样本平均数$\overline{x}$(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)由频数分布表可以认为,本次学科知识竞赛的成绩Z服从正态分布N(μ,196),其中μ近似为样本平均数$\overline{x}$.
①利用该正态分布.求P(Z>74);
②某班级共有20名同学参加此次学科知识比赛,记X表示这20名同学中成绩超过74分的人数,利用①的结果,求EX.附:若Z~N(μ,σ2),则P(μ-σ<Z<+σ)=0.6826,P(μ-2<Z<μ+2σ)=0.9544.
| 组别 | [30,40] | [40,50] | [50,60] | [60,70] | [70,80] | [80,90] | [90,100] |
| 频数 | 3 | 10 | 12 | 15 | 6 | 2 | 2 |
(Ⅱ)由频数分布表可以认为,本次学科知识竞赛的成绩Z服从正态分布N(μ,196),其中μ近似为样本平均数$\overline{x}$.
①利用该正态分布.求P(Z>74);
②某班级共有20名同学参加此次学科知识比赛,记X表示这20名同学中成绩超过74分的人数,利用①的结果,求EX.附:若Z~N(μ,σ2),则P(μ-σ<Z<+σ)=0.6826,P(μ-2<Z<μ+2σ)=0.9544.
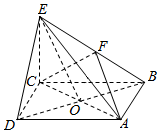 如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.