题目内容
14. 《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )
《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )| A. | 21斛 | B. | 34斛 | C. | 55斛 | D. | 63斛 |
分析 根据米堆的底部的弧度即底面圆周的四分之一为8尺,可求出圆锥的底面半径,从而计算出米堆的体积,用体积除以每斛的体积即可求得斛数.
解答 解:设米堆所在圆锥的底面半径为r尺,
则$\frac{1}{4}$×2πr=8,解得:r=$\frac{16}{π}$,
所以米堆的体积为V=$\frac{1}{4}×\frac{1}{3}$×πr2×5=$\frac{320}{3π}$≈35.56,
所以米堆的斛数是$\frac{35.56}{1.62}$≈21,
故选:A.
点评 考查了圆锥的计算及弧长的计算,解题的关键是从实际问题中抽象出圆锥的知识,难度不大.

练习册系列答案
相关题目
5.已知数列{an}为等差数列,若a12+a102≤25恒成立,则a1+3a7的取值范围为( )
| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
4.若集合A={x∈Z|-2<x<2},B={x|y=log2x2},则A∩B=( )
| A. | {-1,1} | B. | {-1,0,1} | C. | {1} | D. | {0,1} |
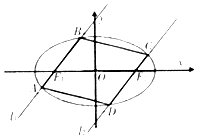 如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.
如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.