题目内容
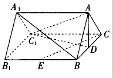 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形,求证CE⊥平面AC1D.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形,求证CE⊥平面AC1D.考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:由直棱柱的特征可得BB1⊥AD,由三角形三线合一可得AD⊥BC,结合线面垂直的判定定理可得AD⊥平面B1BCC1.进而AD⊥CE,由侧面B1BCC1为正方形,D,E分别为BC,BB1的中点,利用三角形全等可证得C1D⊥CE,最后再由线面垂直的判定定理证得CE⊥平面AC1D;
解答:
证明:所以BB1⊥AD.
因为AB=AC,D为BC中点,
所以AD⊥BC.又BC∩BB1=B,
所以AD⊥平面B1BCC1.
又CE?平面B1BCC1,
所以AD⊥CE.
因为四边形B1BCC1为正方形,D,E分别为BC,BB1的中点,
所以Rt△CBE≌Rt△C1CD,∠CC1D=∠BCE.
所以∠BCE+∠C1DC=90°.
所以C1D⊥CE.
又AD∩C1D=D,
所以CE⊥平面AC1D.
因为AB=AC,D为BC中点,
所以AD⊥BC.又BC∩BB1=B,
所以AD⊥平面B1BCC1.
又CE?平面B1BCC1,
所以AD⊥CE.
因为四边形B1BCC1为正方形,D,E分别为BC,BB1的中点,
所以Rt△CBE≌Rt△C1CD,∠CC1D=∠BCE.
所以∠BCE+∠C1DC=90°.
所以C1D⊥CE.
又AD∩C1D=D,
所以CE⊥平面AC1D.
点评:本题以一个特殊的直三棱柱为例,要我们证明线面平行和面面垂直,着重考查了平面与平面垂直的判定定理和直线与平面平移的判定定理,属于中档题

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
当θ为第三象限角时,
-
的值为=( )
| |sinθ| |
| sinθ |
| 2cosθ |
| |cosθ| |
| A、1 | B、-1 | C、3 | D、-3 |
正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,则过A1,M,N三点的平面截正方体所得的截面形状是( )
| A、平行四边形 | B、直角梯形 |
| C、等腰梯形 | D、三角形 |