题目内容
设随机变量ξ服从正态分布N(2,22),且P(ξ<1)=0.1,则P(1<ξ<3)= .
考点:正态分布曲线的特点及曲线所表示的意义
专题:计算题,概率与统计
分析:根据随机变量ξ服从正态分布N(2,22),看出这组数据对应的正态曲线的对称轴x=2,根据正态曲线的特点,得到P(ξ>3)=P(ξ<1),从而得到结果.
解答:
解:∵随机变量X服从正态分布N(2,22),
∴μ=2,得对称轴是x=2.
∵P(ξ<1)=0.1,
∴P(ξ>3)=P(ξ<1)=0.1,
∴P(1<ξ<3)=1-0.2=O.8.
故答案为:O.8.
∴μ=2,得对称轴是x=2.
∵P(ξ<1)=0.1,
∴P(ξ>3)=P(ξ<1)=0.1,
∴P(1<ξ<3)=1-0.2=O.8.
故答案为:O.8.
点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查正态曲线的对称性,考查对称区间的概率相等,本题是一个基础题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
复数z=1+i的虚部是( )
| A、1 | B、-1 | C、i | D、-i |
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,则C的渐近线方程为( )
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| A、y=±2x | ||
B、y=±
| ||
| C、y=±4x | ||
D、y=±
|
已知sin(π+α)=
,且α是第四象限的角,那么cos(α-2π)的值是( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
 已知椭圆
已知椭圆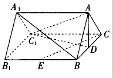 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形,求证CE⊥平面AC1D.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形,求证CE⊥平面AC1D.