题目内容
下列结论错误的是( )
A、若ab>0,则
| ||||
B、函数y=cosx+
| ||||
| C、函数y=2x+2-x的最小值为2 | ||||
D、若x∈(0,1),则函数y=lnx+
|
考点:命题的真假判断与应用
专题:计算题,阅读型,函数的性质及应用,不等式的解法及应用
分析:若ab>0,则
>0,
>0,由基本不等式即可判断A;
令t=cosx(0<x<
),则0<t<1,y=t+
在(0,1)上递减,即可判断B;
令t=2x,则t>0,再由基本不等式,可得最小值,即可判断C;
令t=lnx,则t<0,y=t+
=-[(-t)+
],运用基本不等式即可判断D.
| a |
| b |
| b |
| a |
令t=cosx(0<x<
| π |
| 2 |
| 1 |
| t |
令t=2x,则t>0,再由基本不等式,可得最小值,即可判断C;
令t=lnx,则t<0,y=t+
| 1 |
| t |
| 1 |
| -t |
解答:
解:对于A.若ab>0,则
>0,
>0,则
+
≥2
=2,则A正确;
对于B.令t=cosx(0<x<
),则0<t<1,y=t+
在(0,1)上递减,即有y>2,无最小值,则B错误;
对于C.令t=2x,则t>0,y=2x+2-x=t+
≥2,当且仅当t=1即x=0时,取得最小值2,则C正确;
对于D.令t=lnx,则t<0,则y=t+
=-[(-t)+
]≤-2
=-2,当且仅当t=-1,取得最大值-2,则D正确.
故选B.
| a |
| b |
| b |
| a |
| b |
| a |
| a |
| b |
|
对于B.令t=cosx(0<x<
| π |
| 2 |
| 1 |
| t |
对于C.令t=2x,则t>0,y=2x+2-x=t+
| 1 |
| t |
对于D.令t=lnx,则t<0,则y=t+
| 1 |
| t |
| 1 |
| -t |
-t•
|
故选B.
点评:本题考查基本不等式的运用:求最值,考查余弦函数、指数函数和对数函数的单调性的运用,考查运算能力,属于基础题和易错题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
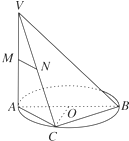 如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )
如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )| A、平面VAC⊥平面VBC |
| B、OC⊥平面VAC |
| C、MN与BC所成的角为45° |
| D、MN∥AB |
已知圆的方程为x2+y2-2xlga+2ylg(10a)+2lg2a+2lga=0(a>0),则圆心所在的直线方程为( )
| A、x-y+1=0 |
| B、x+y+1=0 |
| C、x-y-1=0 |
| D、x+y-1=0 |
若函数y=sin(-2x+φ)(|φ|<
)的图象向左平移
个单位得到y=sin(-2x)的图象,则φ的值为( )
| π |
| 2 |
| π |
| 8 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知△ABC的三个内角分别是A、B、C,那么“sinA>cosB”是△ABC为锐角△的( )
| A、必要而不充分条件 |
| B、充要条件 |
| C、充分而不必要条件 |
| D、既不充分也不必要条件 |
 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B=|x|log2(x+2)<4}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B=|x|log2(x+2)<4}.