题目内容
已知△ABC的三个内角分别是A、B、C,那么“sinA>cosB”是△ABC为锐角△的( )
| A、必要而不充分条件 |
| B、充要条件 |
| C、充分而不必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据三角函数的诱导公式,利用充分条件和必要条件的定义进行判断即可.
解答:
解:当A=
,B=
时,满足sinA>cosB,但此时△ABC是直角角三角形,
∴△ABC是锐角三角形不成立.
当△ABC为锐角三角形时,A+B>
,A>
-B,
∴sinA>sin(
-B)=cosB,
故sinA>cosB成立.
∴“sinA>cosB”是“△ABC为锐角三角形”的必要不充分条件,
故选:A.
| π |
| 2 |
| π |
| 3 |
∴△ABC是锐角三角形不成立.
当△ABC为锐角三角形时,A+B>
| π |
| 2 |
| π |
| 2 |
∴sinA>sin(
| π |
| 2 |
故sinA>cosB成立.
∴“sinA>cosB”是“△ABC为锐角三角形”的必要不充分条件,
故选:A.
点评:本题主要考查充分条件和必要条件的应用,利用三角函数的诱导公式是解决本题的关键.

练习册系列答案
相关题目
下列结论错误的是( )
A、若ab>0,则
| ||||
B、函数y=cosx+
| ||||
| C、函数y=2x+2-x的最小值为2 | ||||
D、若x∈(0,1),则函数y=lnx+
|
下列说法中,正确的是( )
| A、棱柱的侧面可以是三角形 |
| B、有两个面平行,其余各面都是四边形的几何体叫棱柱 |
| C、将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥 |
| D、棱台的侧棱所在的直线交于一点 |
已知正项等比数列{an}中,若a1a3=2,a2a4=4,则a5=( )
| A、±4 | B、4 | C、±8 | D、8 |
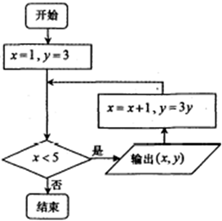 运行如图所示的程序框图,输出的所有实数对(x,y)所对应的点都在某函数图象上,则该函数的解析式为( )
运行如图所示的程序框图,输出的所有实数对(x,y)所对应的点都在某函数图象上,则该函数的解析式为( )| A、y=x+2 | ||
B、y=
| ||
| C、y=3x | ||
| D、y=3x3 |