题目内容
如果sin（3π+θ）=
，求：
+
的值．
| 1 |
| 4 |
| cos(π+θ) |
| cosθ[cos(π+θ)-1] |
| cos(θ-2π) |
| cos(θ+2π)cos(π+θ)+cos(-θ) |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由已知等式求出sinθ的值，原式利用诱导公式化简后，再利用同角三角函数间基本关系整理后，将sinθ的值代入计算即可求出值．
解答：
解：∵sin（3π+θ）=-sinθ=
，即sinθ=-
，
∴原式=
+
=
+
=
=-8．
| 1 |
| 4 |
| 1 |
| 4 |
∴原式=
| -cosθ |
| -cos2θ-cosθ |
| cosθ |
| -cos2θ+cosθ |
| 1 |
| cosθ+1 |
| 1 |
| 1-cosθ |
| 2 |
| sin2θ |
点评：此题考查了运用诱导公式化简求值，以及三角函数的化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
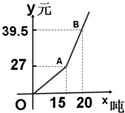自来水公司为鼓励居民节约用水，采取按月用水量分段收费办法，若居民应交水费y（元）与用水量x（吨）的函数关系如图所示．