题目内容
 一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是
一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:先由条件求得灯不亮的概率,再用1减去此概率,即得所求.
解答:
解:开关C断开的概率为
,开关D断开的概率为
,开关A、B至少一个断开的概率为1-
×
=
,
开关E、F至少一个断开的概率为1-
×
=
,
故灯不亮的概率为
×
×
×
=
,
故灯亮的概率为1-
=
,
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
开关E、F至少一个断开的概率为1-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故灯不亮的概率为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 64 |
故灯亮的概率为1-
| 9 |
| 64 |
| 55 |
| 64 |
故选:B.
点评:本题主要考查相互独立事件的概率乘法公式,等可能事件的概率,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
设点P在曲线ρsinθ=2上,点Q在曲线ρ=-2cosθ上,则|PQ|的最小值为( )
| A、2 | B、1 | C、3 | D、0 |
若a>b,则下列各项正确的是( )
| A、ac>bc |
| B、ax2>bx2 |
| C、a2>b2 |
| D、a2x>b2x |
角α的终边过点P(-4,3),则sin2α=( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
在空间直角坐标系中,点P(3,-2,1)关于y对称的点的坐标是( )
| A、(3,2,-1) |
| B、(-3,-2,-1) |
| C、(-3,2,-1) |
| D、(-3,2,-1) |
正方体ABCD-A1B1C1D1的面BCC1B1内有一点M,满足∠MD1D=∠BD1D,则点M的轨迹是( )
| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
将点P(-2,2)变换为P′(-6,1)的伸缩变换公式为( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
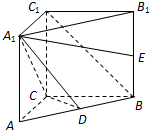 (理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=
(理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=