题目内容
已知α∈(-
,0),cos(π+α)=-
,则tanα=( )
| π |
| 2 |
| 2 |
| 3 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用诱导公式求得cosα 的值,再利用同角三角函数的基本关系求得sinα的值,进而求得tanα=
的值.
| sinα |
| cosα |
解答:
解:∵α∈(-
,0),cos(π+α)=-
=-cosα,∴cosα=
,∴sinα=-
,
则tanα=
=-
,
故选:D.
| π |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
则tanα=
| sinα |
| cosα |
| ||
| 2 |
故选:D.
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知偶函数f(x)的定义域为R,则下列函数中为奇函数的是( )
| A、sin[f(x)] |
| B、x•f(sinx) |
| C、f(x)•f(sinx) |
| D、[f(sinx)]2 |
若a>b,则下列各项正确的是( )
| A、ac>bc |
| B、ax2>bx2 |
| C、a2>b2 |
| D、a2x>b2x |
在△ABC中,角A、B、C所对的边分别为a,b,c,且a>b,则正确的是( )
| A、sinA>sinB且cosA>cosB |
| B、sinA<sinB且cosA<cosB |
| C、sinA>sinB且cosA<cosB |
| D、sinA<sinB且cosA>cosB |
角α的终边过点P(-4,3),则sin2α=( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
正方体ABCD-A1B1C1D1的面BCC1B1内有一点M,满足∠MD1D=∠BD1D,则点M的轨迹是( )
| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
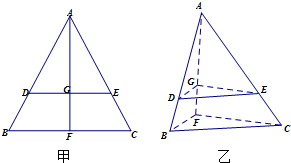 在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.
在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.