题目内容
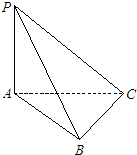 如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=
如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=| 3 |
(1)求直线PC与平面ABC所成角的大小;
(2)求证:平面PAB⊥平面PBC.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)首先找到直线PC与平面ABC所成角就是∠PCA,再根据勾股定理求出AC,问题得以解决.
(2)要证明平面PAB⊥平面PBC,只需要证BC⊥平面PAB,只需要证PA⊥BC,AB⊥BC,由已知条件可证.
(2)要证明平面PAB⊥平面PBC,只需要证BC⊥平面PAB,只需要证PA⊥BC,AB⊥BC,由已知条件可证.
解答:
 解(1)∵PA⊥平面ABC,AC?平面ABC
解(1)∵PA⊥平面ABC,AC?平面ABC
∴PA⊥AC,
∴∠PCA就是直线PC与平面ABC所成角,
又AB⊥BC,AB=1,BC=
,
∴AC=
=2
又PA=2,
在Rt△PAC中,
∴∠PCA45°
证明(2)∵PA⊥平面ABC,BC?平面ABC
∴PA⊥BC,
又AB⊥BC,PA∩AB=A,
∴BC⊥平面PAB,
∵BC?平面PBC
∴平面PAB⊥平面PBC.
 解(1)∵PA⊥平面ABC,AC?平面ABC
解(1)∵PA⊥平面ABC,AC?平面ABC∴PA⊥AC,
∴∠PCA就是直线PC与平面ABC所成角,
又AB⊥BC,AB=1,BC=
| 3 |
∴AC=
| AB2+BC2 |
又PA=2,
在Rt△PAC中,
∴∠PCA45°
证明(2)∵PA⊥平面ABC,BC?平面ABC
∴PA⊥BC,
又AB⊥BC,PA∩AB=A,
∴BC⊥平面PAB,
∵BC?平面PBC
∴平面PAB⊥平面PBC.
点评:本题主要考查了线面角求法和面面垂直的判定定理,识图是关键,属于中档题.

练习册系列答案
相关题目
将点P(-2,2)变换为P′(-6,1)的伸缩变换公式为( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
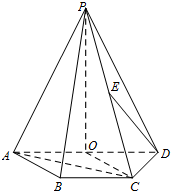 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.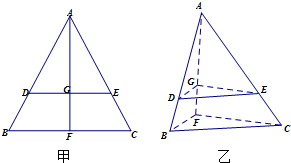 在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.
在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.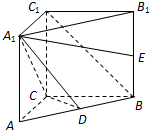 (理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=
(理科)如图,在直三棱柱ABC-A1B1C1中,∠ACB=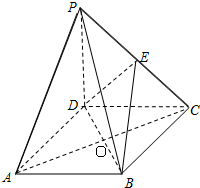 如图,在四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是边长为a的正方形,对角线AC与BD相交于O,且PD=a,E为棱PC的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是边长为a的正方形,对角线AC与BD相交于O,且PD=a,E为棱PC的中点.