题目内容
7.已知$cos(\frac{π}{2}+φ)=\frac{3}{5}$,且$|φ|<\frac{π}{2}$,则tanφ为( )| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
分析 利用同角三角函数的基本关系的应用,以及三角函数在各个象限中的符号,求得tanφ的值.
解答 解:∵已知$cos(\frac{π}{2}+φ)=\frac{3}{5}$=-sinφ,且$|φ|<\frac{π}{2}$,
∴sinφ=-$\frac{3}{5}$,cosφ=$\sqrt{{1-sin}^{2}φ}$=$\frac{4}{5}$,
则tanφ=$\frac{sinφ}{cosφ}$=-$\frac{3}{4}$,
故选:C.
点评 本题主要考查同角三角函数的基本关系的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
15.函数y=9-x2( )
| A. | 有最大值-9 | B. | 有最小值9 | C. | 有最大值9 | D. | 有最小值-9 |
12.若M∪{1}={1,2,3},则M集合可以是( )
| A. | {1,2,3} | B. | {1,3} | C. | {1,2} | D. | {1} |
19.偶函数f(x)在[0,+∞)上单调递增,若f(1)=0,则不等式f(x)>0的解集是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(1,+∞) |
7.从四面体ABCD的6条棱的中点及其四个顶点共10个点中任取4个点,则这四个点不共面的概率是( )
| A. | $\frac{5}{7}$ | B. | $\frac{7}{10}$ | C. | $\frac{24}{35}$ | D. | $\frac{47}{70}$ |
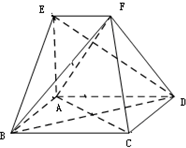 在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.
在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.