题目内容
9.圆x2+(y-m)2=5与双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线相切,则正实数m=( )| A. | 5 | B. | 1 | C. | 5$\sqrt{5}$ | D. | $\sqrt{5}$ |
分析 求出圆的圆心与半径,双曲线的渐近线方程,利用圆与双曲线的渐近线相切列出方程求解即可.
解答 解:圆x2+(y-m)2=5的圆心(0,m),半径为:$\sqrt{5}$,双曲线x2-$\frac{{y}^{2}}{4}$=1的一条渐近线方程为:2x+y=0,圆x2+(y-m)2=5与双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线相切,
可得:$\frac{|m|}{\sqrt{{2}^{2}+{1}^{2}}}=\sqrt{5}$,
解得m=±5,则正实数m=5.
故选:A.
点评 本题考查双曲线与圆的位置关系的综合应用,考查点到直线的距离公式的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
20.已知圆C:x2+y2+2x-3=0,直线l:x+ay+2-a=0(a∈R),则( )
| A. | l与C相离 | B. | l与C相切 | ||
| C. | l与C相交 | D. | 以上三个选项均有可能 |
14.已知实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+2y≤6\\ 3x+y≤12\end{array}\right.$,且x,y∈Z,则z=2x+y的最大值是( )
| A. | 7 | B. | 8 | C. | $\frac{42}{5}$ | D. | 9 |
1.执行如图所示的程序框图,则输出s的值为( )
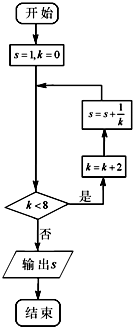

| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{23}{12}$ | D. | $\frac{49}{24}$ |
19.偶函数f(x)在[0,+∞)上单调递增,若f(1)=0,则不等式f(x)>0的解集是( )
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(1,+∞) |
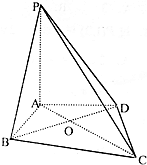 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.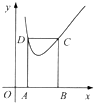 如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.
如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.